

Last updated at December 16, 2024 by Teachoo



Transcript
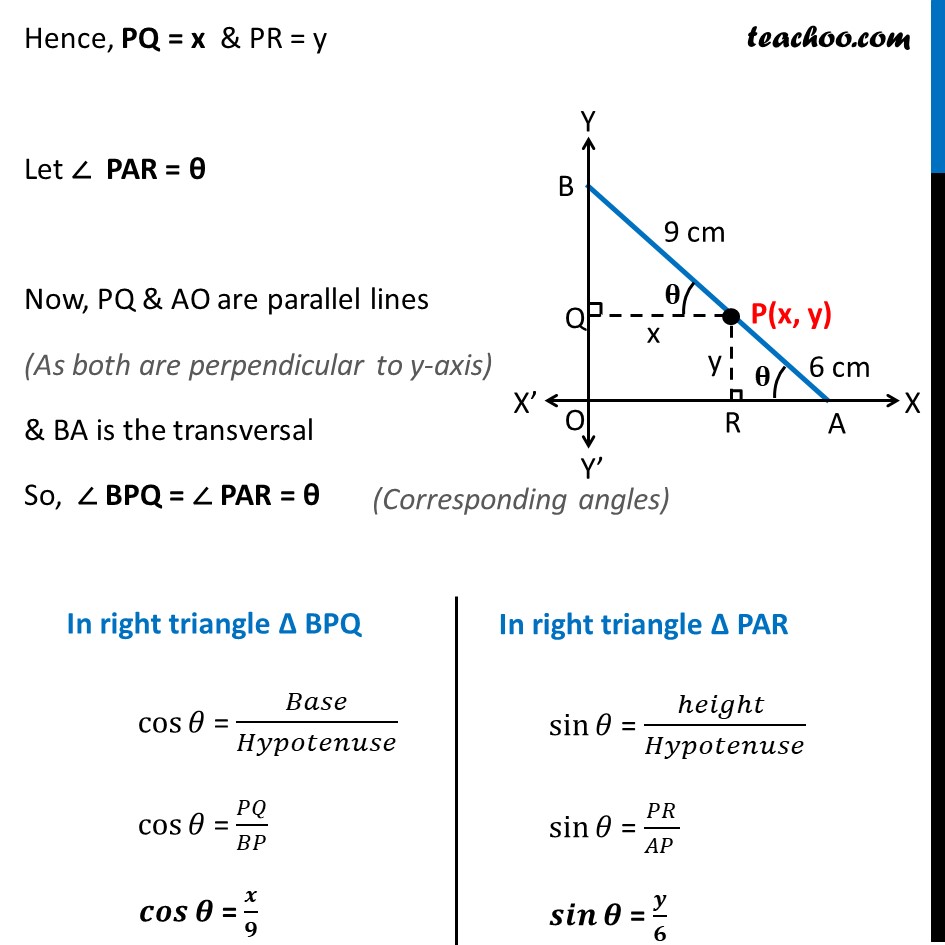
Example 19 A rod AB of length 15 cm rests in between two coordinate axes in such a way that the end point A lies on x-axis and end point B lies on y-axis. A point P(x, y) is taken on the rod in such a way that AP = 6 cm. Show that the locus of P is an ellipse. Given AB = 15 cm & AP = 6 cm Now, PB = AB – AP PB = 15 – 6 PB = 9cm Drawing PQ ⊥ BO and PR ⊥ OA Hence, PQ = x & PR = y Let ∠ PAR = θ Now, PQ & AO are parallel lines (As both are perpendicular to y-axis) & BA is the transversal So ∠ BPQ = ∠ PAR = θ In right triangle ∆ BPQ cos𝜃 = 𝐵𝑎𝑠𝑒/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 cos𝜃 = 𝑃𝑄/𝐵𝑃 𝒄𝒐𝒔𝜽 = 𝒙/𝟗 In right triangle ∆ PAR 〖 sin〗𝜃 = (ℎ𝑒𝑖𝑔ℎ𝑡 )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 〖 sin〗𝜃 = 𝑃𝑅/(𝐴𝑃 ) 〖 𝒔𝒊𝒏〗𝜽 = 𝒚/𝟔 Now we know that, sin2𝜃 + cos2𝜃 = 1 Putting 〖 𝑠𝑖𝑛〗𝜃 = 𝑦/6 and 𝑐𝑜𝑠𝜃 = 𝑥/9 (𝑦/6)^2 + (𝑥/9)^2 = 1 𝑦2/36 + 𝑥2/81 = 1 𝒙𝟐/𝟖𝟏 + 𝒚𝟐/𝟑𝟔 = 1 Hence it satisfies the equation of ellipse 𝑥^2/𝑎^2 + 𝑦^2/𝑏^2 = 1 Thus, locus of P is ellipse Hence proved