Example 18 - Chapter 10 Class 11 Conic Sections

Transcript

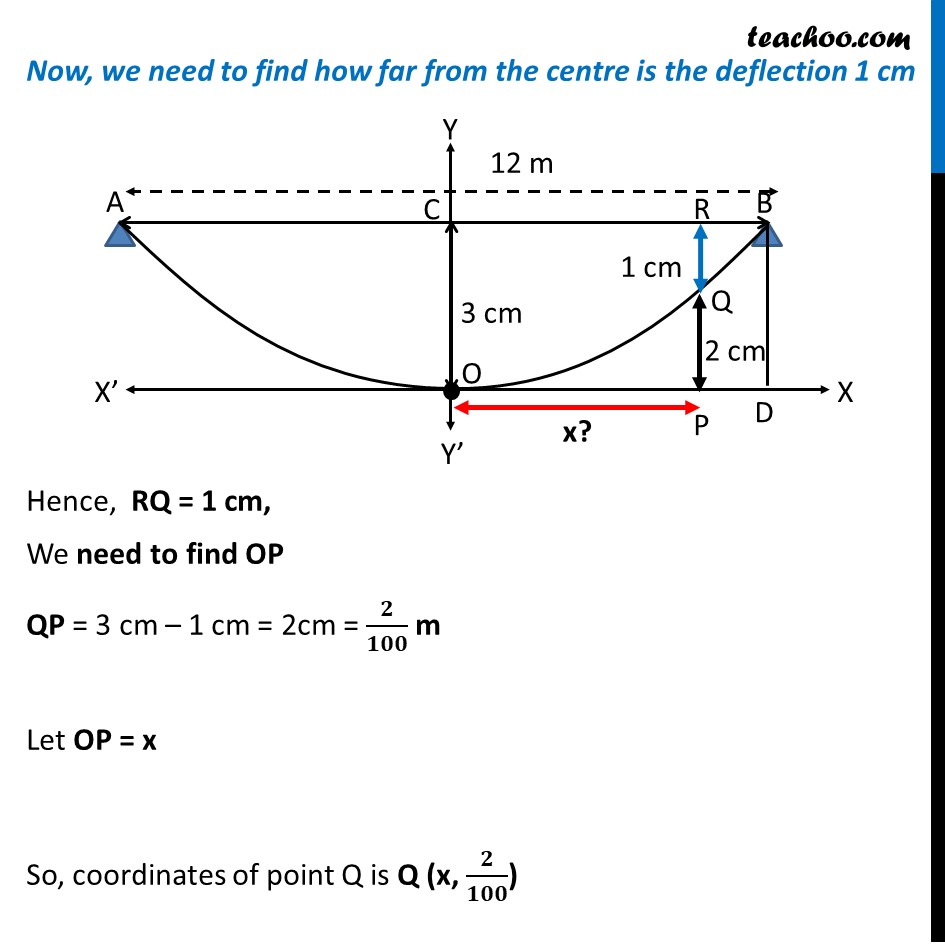
Example 18 A beam is supported at its ends by supports which are 12 metres apart. Since the load is concentrated at its centre, there is a deflection of 3 cm at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the deflection 1 cm? Beam is always facing upwards with the axis vertical Since, the axis is positive y-axis, its equation is x2 = 4ay First we find coordinates of point B Given Width of beam = 12 m Hence, AB = 12 m So, BC = 𝐴𝐵/2 = 12/2 = 6 m Also, there is a deflection of 3 cm from centre So, OC = BD = 3 cm OC = BD = 3 cm = 3/100 m Hence point B is B(6, 𝟑/𝟏𝟎𝟎) Now, Since point B(6, 3/100) lies on the parabola Putting x = 6, y = 3/100 in equation x2 = 4ay (6)2 = 4a (3/100) 36 = (3𝑎 )/25 3/25 a = 36 a = (36 × 25)/3 a = 12 × 25 a = 300 m Now, we need to find how far from the centre is the deflection 1 cm Hence RQ = 1 cm, We need to find OP QP = 3 cm – 1 cm = 2cm = 2/100 m Let OP = x So, coordinates of point Q is Q (x, 𝟐/𝟏𝟎𝟎) Since point Q lies on parabola it will satisfy the equation of parabola Equation of parabola is x2 = 4ay Putting x = x & y = 2/100 m & a = 300 m x2 = 4 (300) (2/100) x2 = 1200 × 2/100 x2 = 24 x = √24 = √(6 ×4) = 2√6 𝑚 Thus, the required distance is 2√𝟔 𝒎