


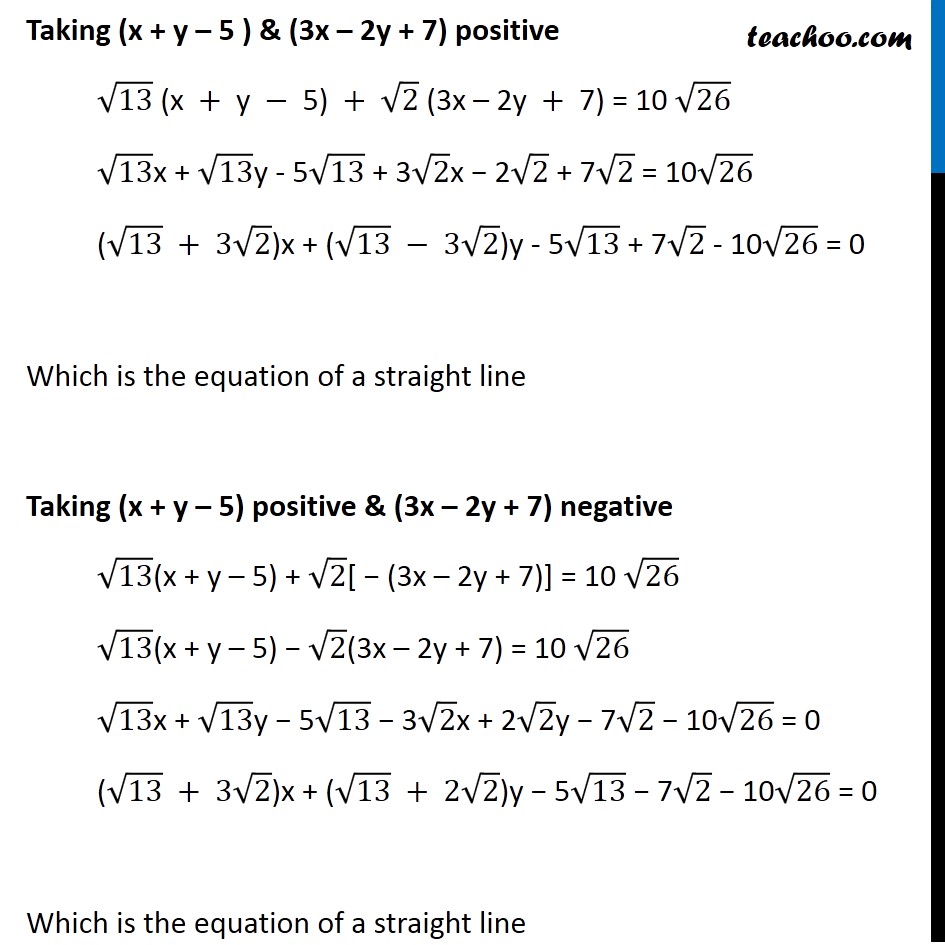


Miscellaneous
Last updated at December 16, 2024 by Teachoo



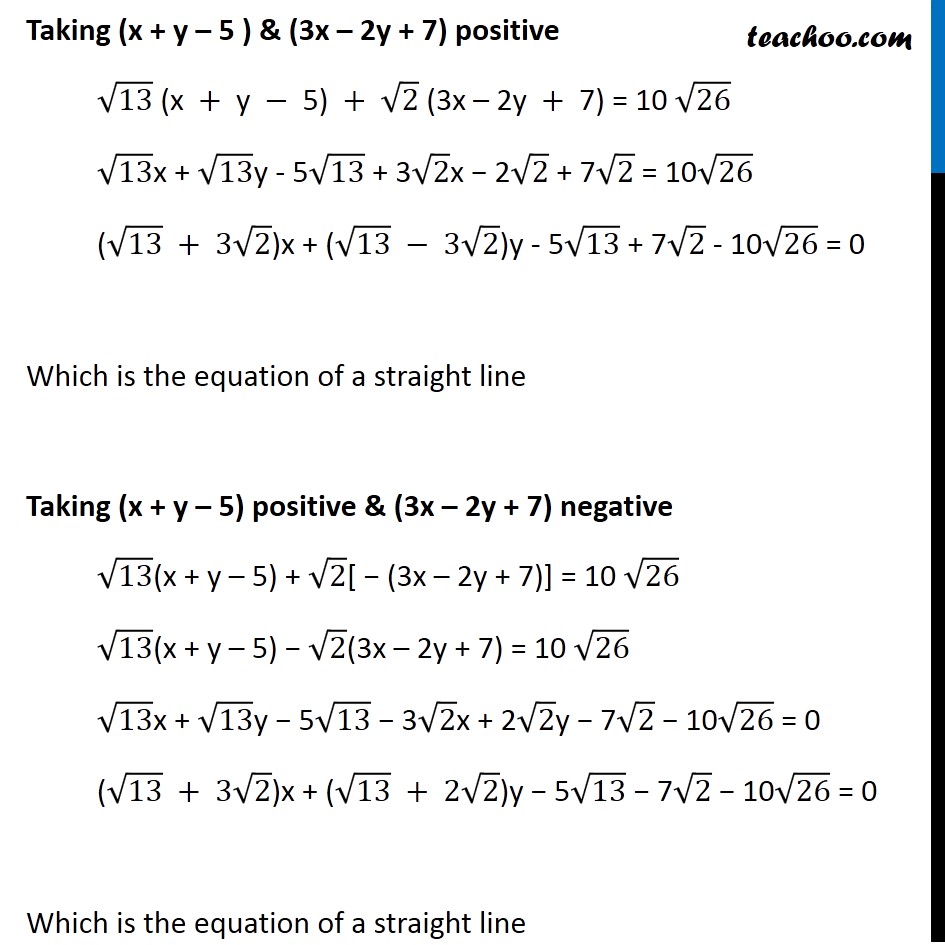


Transcript
Misc 19 If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line. Given lines are x + y – 5 = 0 & 3x – 2y + 7 = 0 We know that , Perpendicular distance of a point (x1, y1) from line Ax + By + C = 0 is d = |〖𝐴𝑥〗_1 + 〖𝐵𝑦〗_1 + 𝐶|/√(𝐴^2 + 𝐵^2 ) Let p1 be the perpendicular distance of point P(x, y) from line x + y – 5 = 0 Here x1 = x , y1 = y & A = 1 , B = 1 , C = − 5 p1 = |1(𝑥) + 1(𝑦) + (−5)|/√((1)^2 + (1)^2 ) = |𝑥 + 𝑦 − 5|/√(1 + 1) = |𝑥 + 𝑦 − 5|/√2 Let p2 be the perpendicular distance from point P(x, y) from line 3x – 2y + 7 = 0 is Here x1 = x , y1 = y & A = 3 , B = –2 , C = 7 p2 = |3(𝑥) − 2(𝑦) − (7)|/√((3)^2 + ( − 2)^2 ) = |3𝑥 − 2𝑦 − 7|/√(9 + 4) = |3𝑥 − 2𝑦 − 7|/√13 Given that Sum of perpendicular distance = 10 p1 + p2 = 10 |𝑥 + 𝑦 − 5|/√2 + |3𝑥 − 2𝑦 + 7|/√13 = 10 (√13 |𝑥 + 𝑦 − 5| + √2 |3𝑥 − 2𝑦 + 7|)/(√2 × √13) = 10 √13 |"(x" + "y" − "5)" | + √2 |"(3x – 2y" + "7)" | = 10 × √13 × √2 √13 |"(x" + "y" − "5)" | + √2 |"(3x – 2y" + "7)" | = 10 √26 We will get 4 cases by solving this equation 1. Taking (x + y – 5 ) & (3x – 2y + 7) positive 2. Taking (x + y – 5) positive & (3x – 2y + 7) negative 3. Taking (x + y – 5) negative & (3x – 2y + 7) positive 4. Taking both (x + y – 5) & (3x – 2y + 7) negative Now, solving separately Taking (x + y – 5 ) & (3x – 2y + 7) positive √13 "(x" + "y" − "5)" + √2 "(3x – 2y" + "7)" = 10 √26 √13x + √13y - 5√13 + 3√2x − 2√2 + 7√2 = 10√26 (√13 + 3√2)x + (√13 − 3√2)y - 5√13 + 7√2 - 10√26 = 0 Which is the equation of a straight line Taking (x + y – 5) positive & (3x – 2y + 7) negative √13(x + y – 5) + √2[ − (3x – 2y + 7)] = 10 √26 √13(x + y – 5) − √2(3x – 2y + 7) = 10 √26 √13x + √13y − 5√13 − 3√2x + 2√2y − 7√2 − 10√26 = 0 (√13 + 3√2)x + (√13 + 2√2)y − 5√13 − 7√2 − 10√26 = 0 Which is the equation of a straight line Taking (x + y – 5) negative & (3x – 2y + 7) positive −√13 (x + y – 5) + √2 (3x – 2y + 7) = 10 √26 −√13x + √13y + 5√13 + 3√2x − 2√2y + 7√2 − 10√26 = 0 (−√13+3√2)x + (− √13 − 2√2)y + 5√13 +7√2 − 10√26 = 0 Which is the equation of a straight line Taking √𝟏𝟑 (x + y – 5) & √𝟐 (3x – 2y + 7) both negative −√13(x + y − 5) − √2(3x − 2y + 7) = 10 √26 −√13x − √13y + 5√13 − 3√2x + 2√2y − 7√2 − 10√26 = 0 (−√13−3√2)x + (−√13+2√2)y + 5√13 − 7√2 − 10√26 = 0 Which is the equation of a straight line Thus, from all 4 cases point P(x, y) moves on a straight line Hence proved