Misc 16 - Chapter 10 Class 11 Straight Lines (Term 1)

Transcript

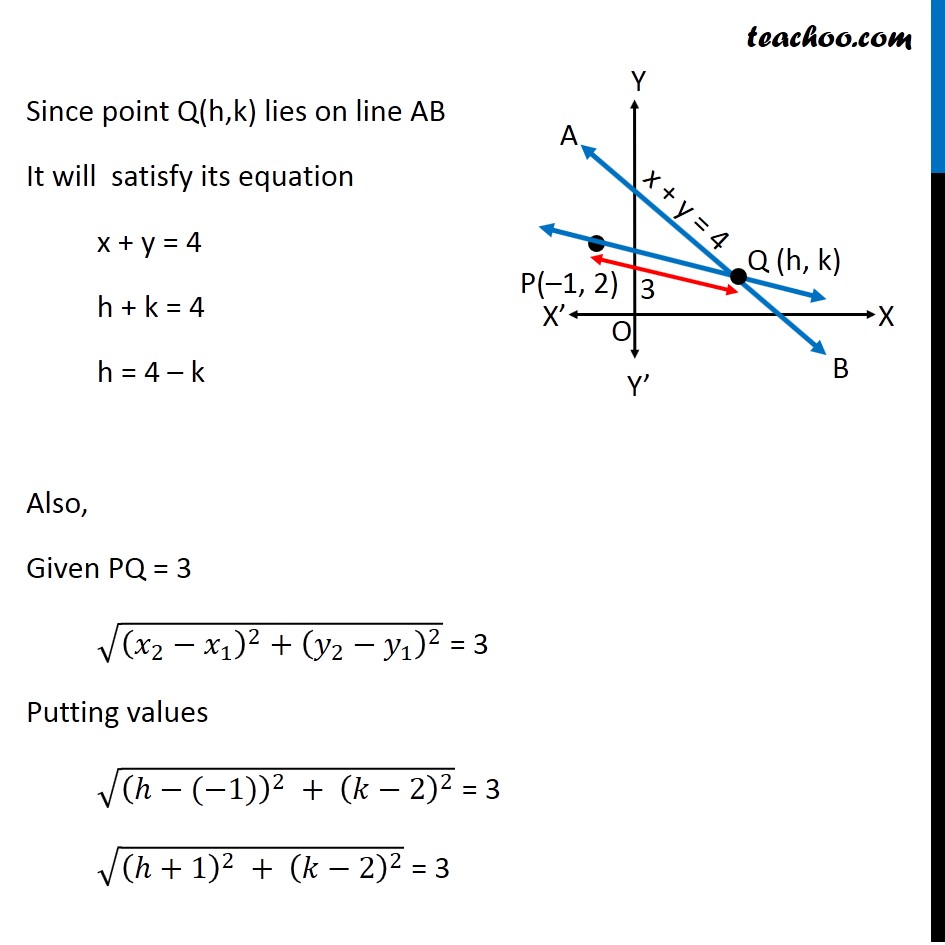
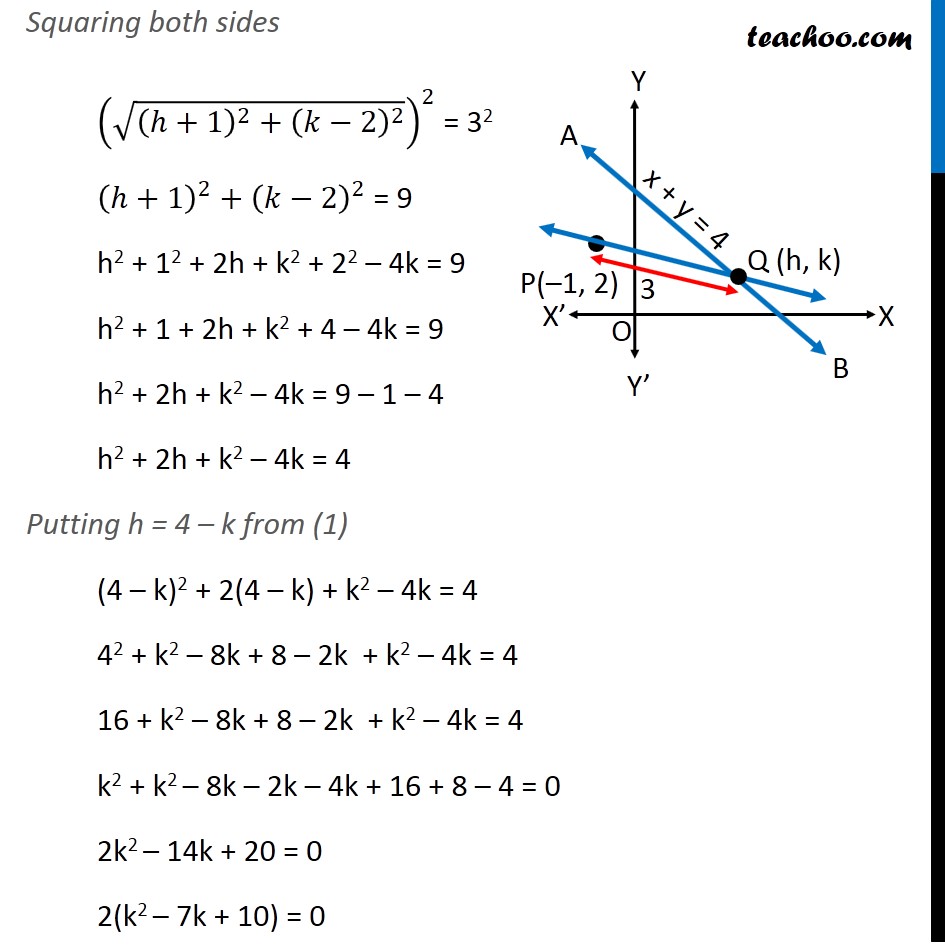
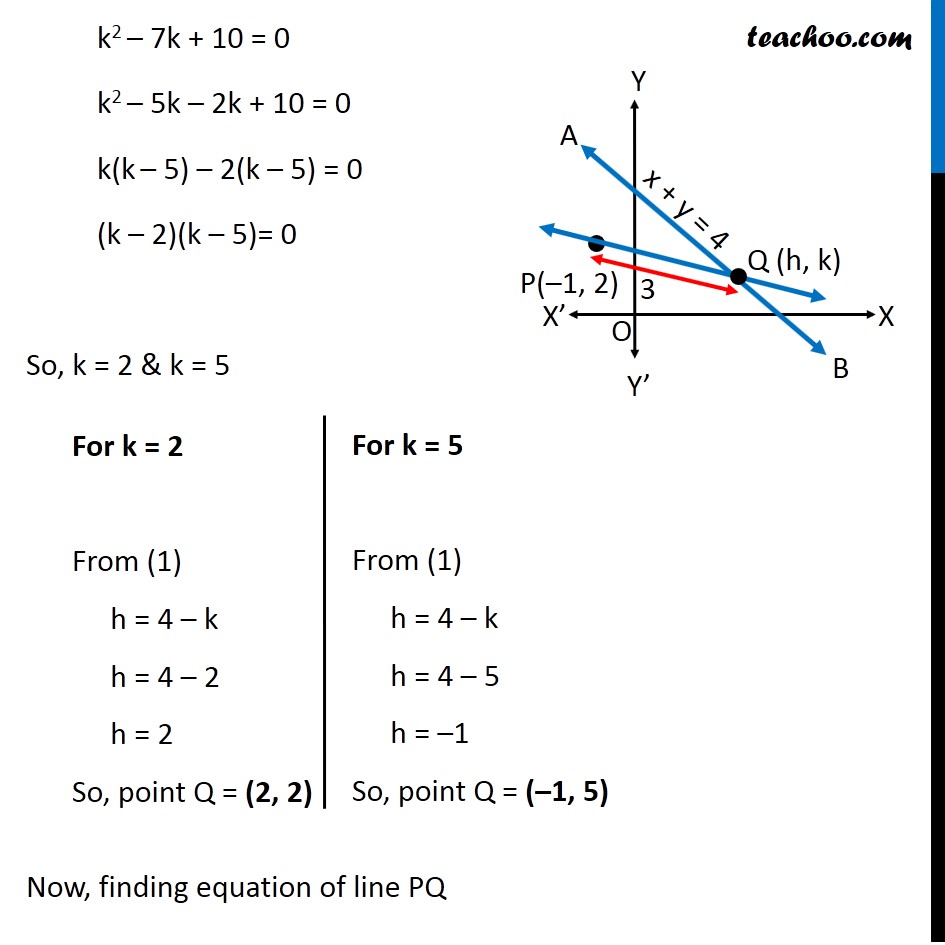
Misc 16 Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point. Let line AB be x + y = 4 & point P be (–1, 2) Q is the point of intersection of line through P(-1, 2) to AB & PQ = 3 units We need to find the equation of line PQ First we will find the co-ordinates of point Q Since point Q(h,k) lies on line AB It will satisfy its equation x + y = 4 h + k = 4 h = 4 – k Also, Given PQ = 3 √((𝑥_2 − 𝑥_1 )^2 + (𝑦_2 − 𝑦_1 )^2 ) = 3 Putting values √((ℎ−(−1))^2 + (𝑘−2)^2 ) = 3 √((ℎ+1)^2 + (𝑘−2)^2 ) = 3 Squaring both sides (√((ℎ+1)^2 + (𝑘−2)^2 ))^2 = 32 (ℎ+1)^2 + (𝑘−2)^2 = 9 h2 + 12 + 2h + k2 + 22 – 4k = 9 h2 + 1 + 2h + k2 + 4 – 4k = 9 h2 + 2h + k2 – 4k = 9 – 1 – 4 h2 + 2h + k2 – 4k = 4 Putting h = 4 – k from (1) (4 – k)2 + 2(4 – k) + k2 – 4k = 4 42 + k2 – 8k + 8 – 2k + k2 – 4k = 4 16 + k2 – 8k + 8 – 2k + k2 – 4k = 4 k2 + k2 – 8k – 2k – 4k + 16 + 8 – 4 = 0 2k2 – 14k + 20 = 0 2(k2 – 7k + 10) = 0 k2 – 7k + 10 = 0 k2 – 5k – 2k + 10 = 0 k(k – 5) – 2(k – 5) = 0 (k – 2)(k – 5)= 0 So, k = 2 & k = 5 Now, finding equation of line PQ We know that equation of line joining two point (x1, y1) & (x2, y2) is (y – y1) = (𝑦2 − 𝑦1)/(𝑥2 − 𝑥1) (x – x1) So, line is parallel to x axis or y -axis