You are here
Misc 13 - Chapter 9 Class 11 Straight Lines
Last updated at Dec. 16, 2024 by Teachoo
Chapter 9 Class 11 Straight Lines
Concept wise
- Cordinate geometry questions
- Slope - Finding slope
- Slope - Prependicularity
- Angle between two lines by Slope
- Collinearity of 3 points by sliope
- Point Slope form
- Slope-Intercept form
- Intercept form
- Normal form
- Given Statement
-
Two lines // or/and prependicular
- Angle between two lines
- Distance - Between two parallel lines
- Distance of a point from a line
- Distance of a point from a line along a line
- Other Type of questions - Area of Triangle formed
- Other Type of questions - 3 lines Concurrent
- Other Type of questions - Image
- Other Type of questions - Mix
Transcript
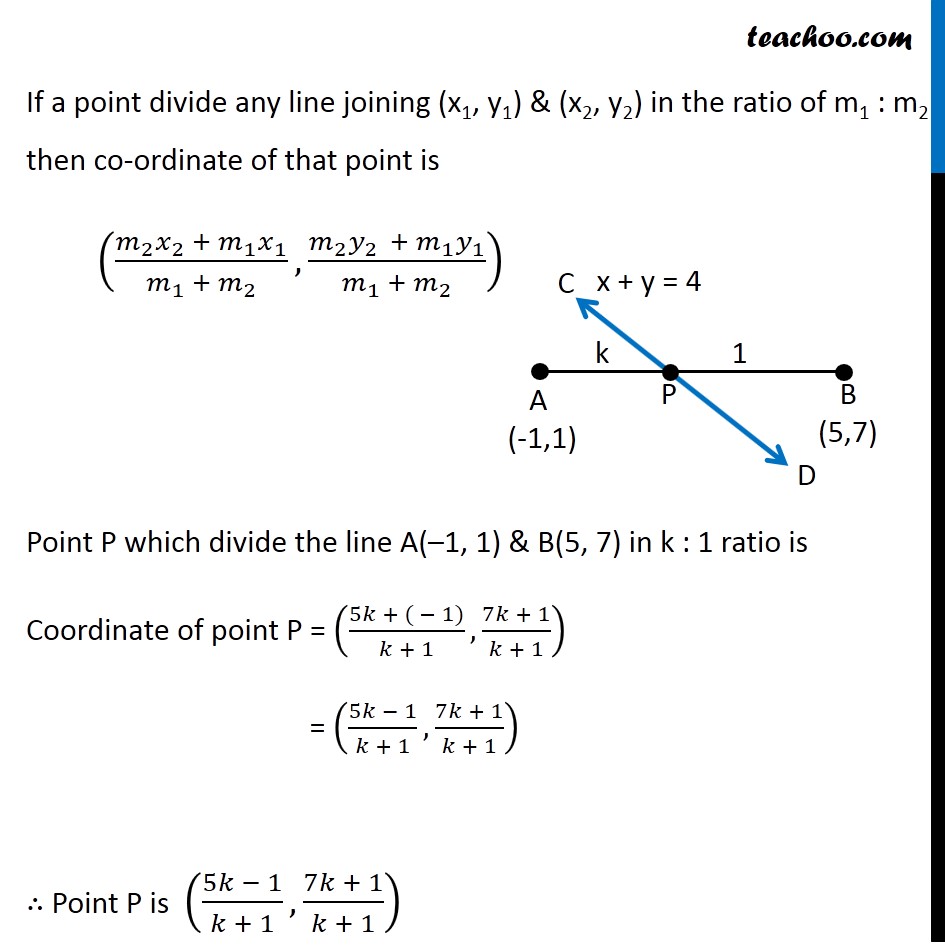
Misc 13 In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4? Let line AB is the line joining the points A(–1, 1) & B(5, 7) & let line CD be x + y = 4 Let line AB be divided by the line CD at point P Let k :1 be the ratio line AB is divided by the line CD We need to find value of k If a point divide any line joining (x1, y1) & (x2, y2) in the ratio of m1 : m2 then co-ordinate of that point is ((𝑚_2 𝑥_2 + 𝑚_1 𝑥_1)/(𝑚_1 + 𝑚_2 ),(𝑚_2 𝑦_(2 ) + 𝑚_1 𝑦_1)/(𝑚_1 + 𝑚_2 )) Point P which divide the line A(–1, 1) & B(5, 7) in k : 1 ratio is Coordinate of point P = ((5𝑘 + ( − 1))/(𝑘 + 1), (7𝑘 + 1)/(𝑘 + 1)) = ((5𝑘 − 1)/(𝑘 + 1), (7𝑘 + 1)/(𝑘 + 1)) ∴ Point P is ((5𝑘 − 1)/(𝑘 + 1), (7𝑘 + 1)/(𝑘 + 1)) Now, point P((5𝑘 − 1)/(𝑘 + 1), (7𝑘 + 1)/(𝑘 + 1)) lies on the line CD So, It will satisfy the equation of line CD So, x + y = 4 Putting x = (5𝑘 − 1)/(𝑘 + 1), y = (7𝑘 + 1)/(𝑘 + 1) ((5𝑘 − 1)/(𝑘 + 1)) + ((7𝑘 + 1)/(𝑘 + 1)) = 4 ((5𝑘 − 1) + (7𝑘 + 1))/(𝑘 + 1) = 4 5k – 1 + 7k + 1 = 4(k + 1) 5k + 7k – 1 + 1 = 4k + 4 12k + 0 = 4k + 4 12k – 4k = 4 8k = 4 k = 4/8 k = 1/2 Hence, Point P divides AB in the ratio of k : 1 = 1/2 : 1 = 2 × 1/2 : 2 × 1 = 1 : 2 Thus , required ratio is 1 : 2
