Misc 7 - Chapter 9 Class 11 Straight Lines

Transcript

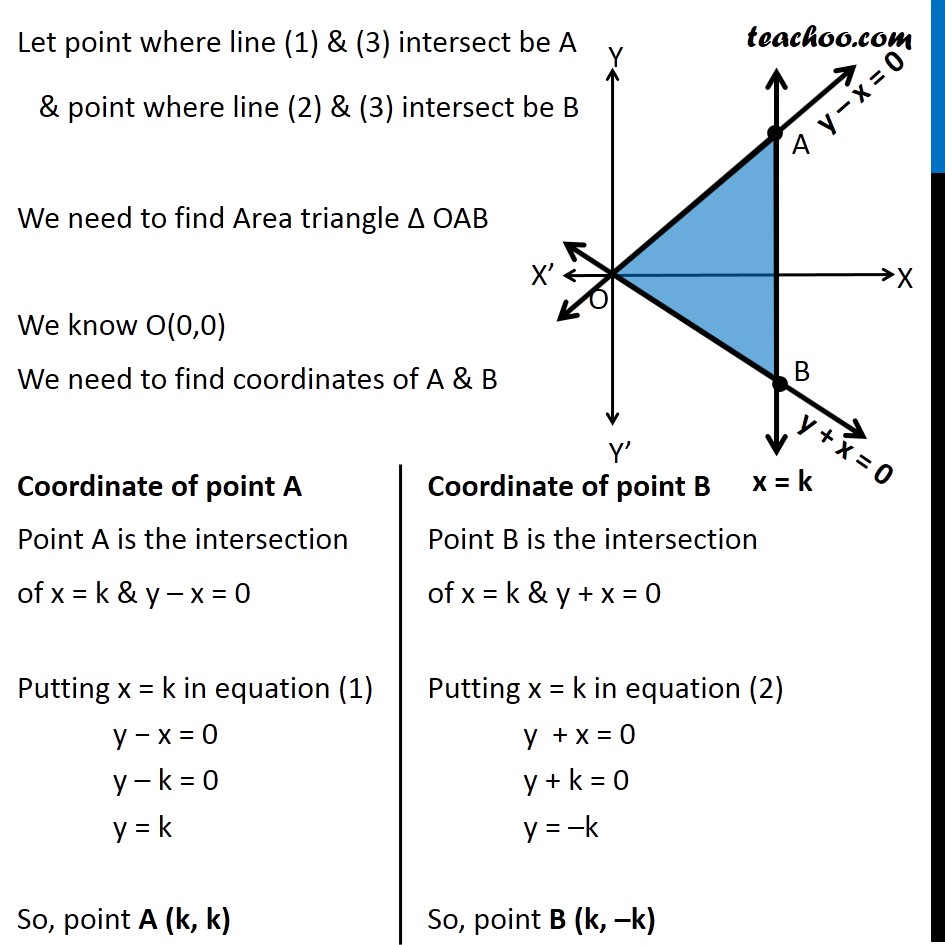
Let point where line (1) & (3) intersect be A & point where line (2) & (3) intersect be B We need to find Area triangle Δ OAB We know O(0,0) We need to find coordinates of A & B Coordinate of point A Point A is the intersection of x = k & y – x = 0 Putting x = k in equation (1) y − x = 0 y – k = 0 y = k So, point A (k, k) Coordinate of point B Point B is the intersection of x = k & y + x = 0 Putting x = k in equation (2) y + x = 0 y + k = 0 y = –k So, point B (k, –k) We know that Area of triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is = 1/2 |𝑥1(𝑦2 − 𝑦3) + 𝑥2(𝑦3 − 𝑦1) + 𝑥3 (𝑦1 − 𝑦2)| For ∆ AOB, (x1, y1) = O(0, 0) (x2,y2) = A(k, k) (x3,y3) = B(k, –k) Area of triangle ∆OAB whose vertices are (0, 0) (k, k) & (k, − k) = 1/2 |0(𝑘−(− 𝑘))+𝑘(−𝑘 −0) 𝑘(0−𝑘)| = 1/2 |0(k−(− k))+k(−k −0) k(0−k)| = 1/2 |0+k(−k)+k(−k)| = 1/2 |−k2−k2| = 1/2 |−2k2| = 2k2/2 = k2 square units Hence, required area of triangle is k2 square units