Misc 5 - Chapter 10 Class 11 Straight Lines (Important Question)

Transcript

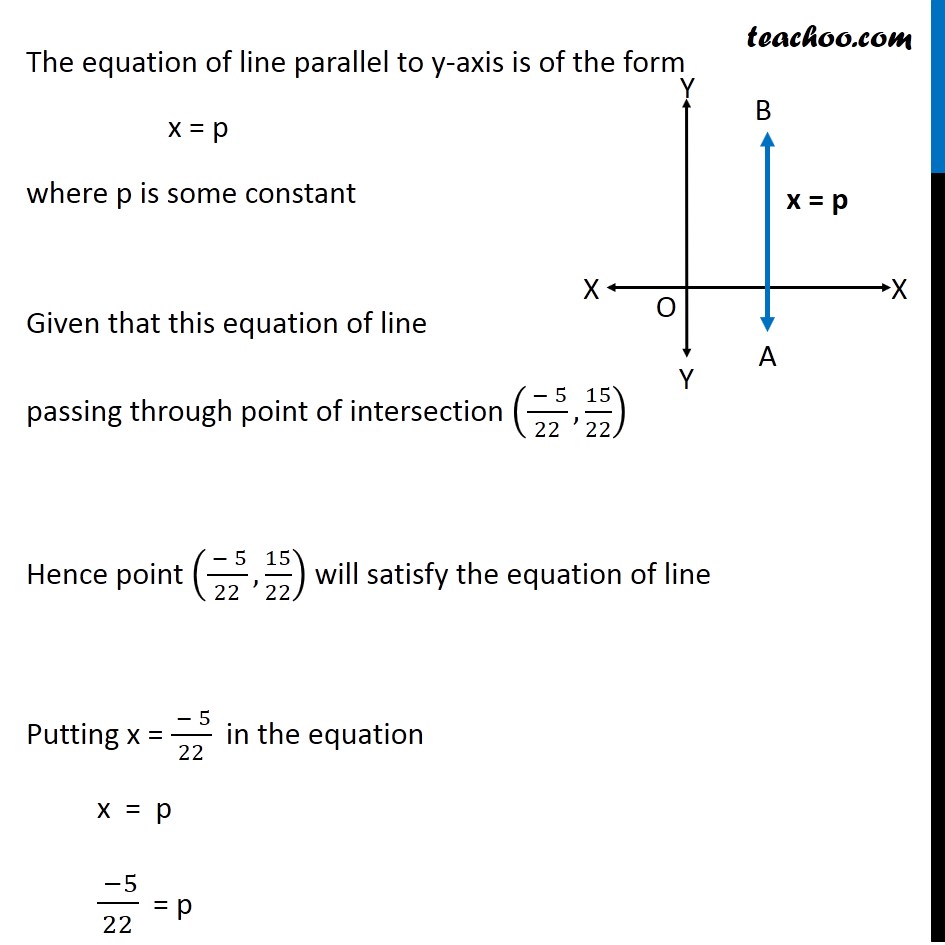
Misc 5 Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0. First we calculate point of intersection of lines x – 7y + 5 = 0 & 3x + y = 0 Solving (1) x – 7y + 5 = 0 x = 7y − 5 Putting value of x in (2) 3x + y = 0 3(7y − 5) + y = 0 21y − 15 + y = 0 21y + y − 15 = 0 22y − 15 = 0 22y = 15 y = 15/22 Putting value of y = 15/22 in (1) x – 7y + 5 = 0 x – 7(15/22) + 5 = 0 x = 7(15/22) − 5 x = (15 × 7 − 22 × 5)/22 x = (105 − 110)/22 x = ( −5)/22 Hence point of intersection is (( −5)/22, 15/22) The equation of line parallel to y-axis is of the form x = p where p is some constant Given that this equation of line passing through point of intersection (( − 5)/22, 15/22) Hence point (( − 5)/22, 15/22) will satisfy the equation of line Putting x = ( − 5)/22 in the equation x = p ( −5)/22 = p p = ( −5)/22 Thus, Required equation of line is x = p Putting values x = ( −𝟓)/𝟐𝟐