You are here
Misc 1 - Chapter 9 Class 11 Straight Lines
Last updated at Dec. 16, 2024 by Teachoo
Chapter 9 Class 11 Straight Lines
Concept wise
- Cordinate geometry questions
- Slope - Finding slope
- Slope - Prependicularity
- Angle between two lines by Slope
- Collinearity of 3 points by sliope
- Point Slope form
-
Slope-Intercept form
- Intercept form
- Normal form
- Given Statement
- Two lines // or/and prependicular
- Angle between two lines
- Distance - Between two parallel lines
- Distance of a point from a line
- Distance of a point from a line along a line
- Other Type of questions - Area of Triangle formed
- Other Type of questions - 3 lines Concurrent
- Other Type of questions - Image
- Other Type of questions - Mix
Transcript
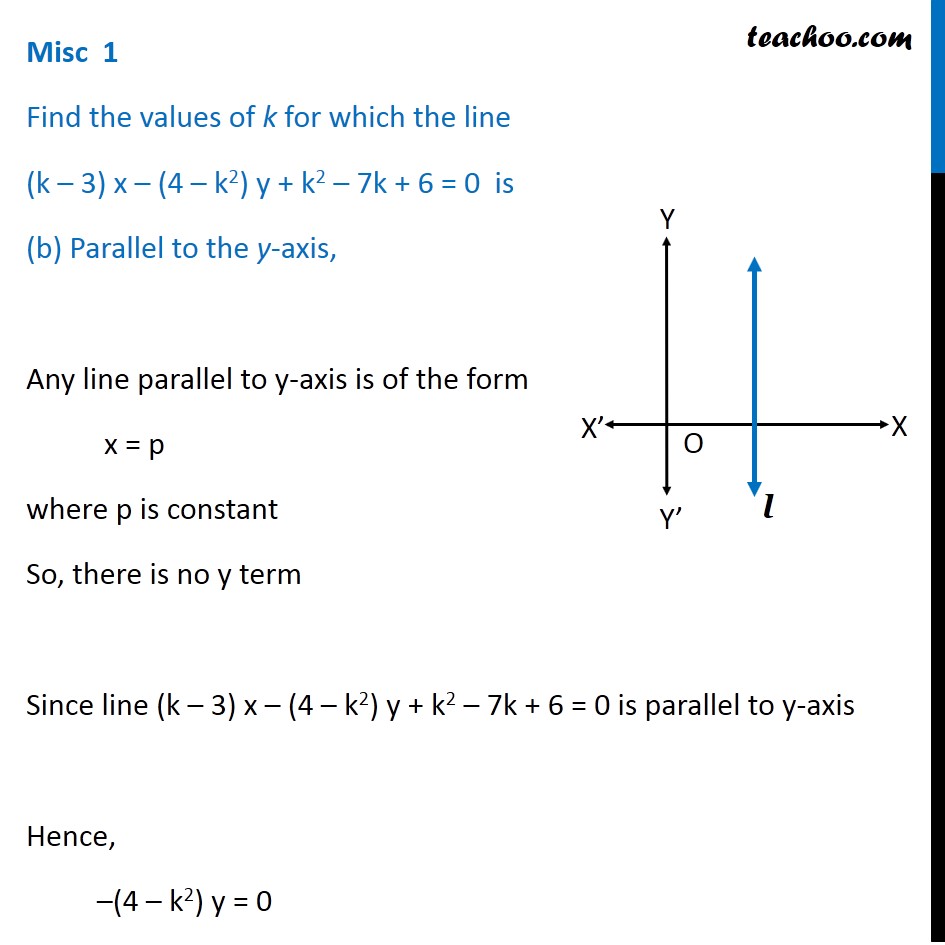
Misc 1 Find the values of k for which the line (k – 3) x – (4 – k2)y + k2 – 7k + 6 = 0 is Parallel to the x-axis, Any line parallel to x-axis is of the form y = p where p is constant So, there is no x term Since Line (k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 is parallel to x-axis Hence, (k − 3)x = 0 k – 3 = 0/𝑥 k – 3 = 0 k = 3 Misc 1 Find the values of k for which the line (k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 is (b) Parallel to the y-axis, Any line parallel to y-axis is of the form x = p where p is constant So, there is no y term Since line (k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 is parallel to y-axis Hence, –(4 – k2) y = 0 −(4 − k2) = 0/𝑦 –4 + k2 = 0 k2 = 4 k = ± √4 k = ± 2 Hence k = 2 or −2 Misc 1 Find the values of k for which the line (k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 is (c) Passing through origin If the line passing through the origin i.e. (0, 0) will satisfy the equation of line Putting x = 0 & y = 0 in equation (k − 3)x − (4 − k2)y + k2 − 7k + 6 = 0 (k − 3)0 − (4 − k2)0 + k2 − 7k + 6 = 0 k2 − 7k + 6 = 0 k2 − 6k − k + 6 = 0 k(k − 6) − 1(k − 6) = 0 k(k − 6) − 1(k − 6) = 0 (k − 1)(k − 6) = 0 So, k = 1 or k = 6
