Ex 9.3, 13 - Chapter 9 Class 11 Straight Lines

Transcript

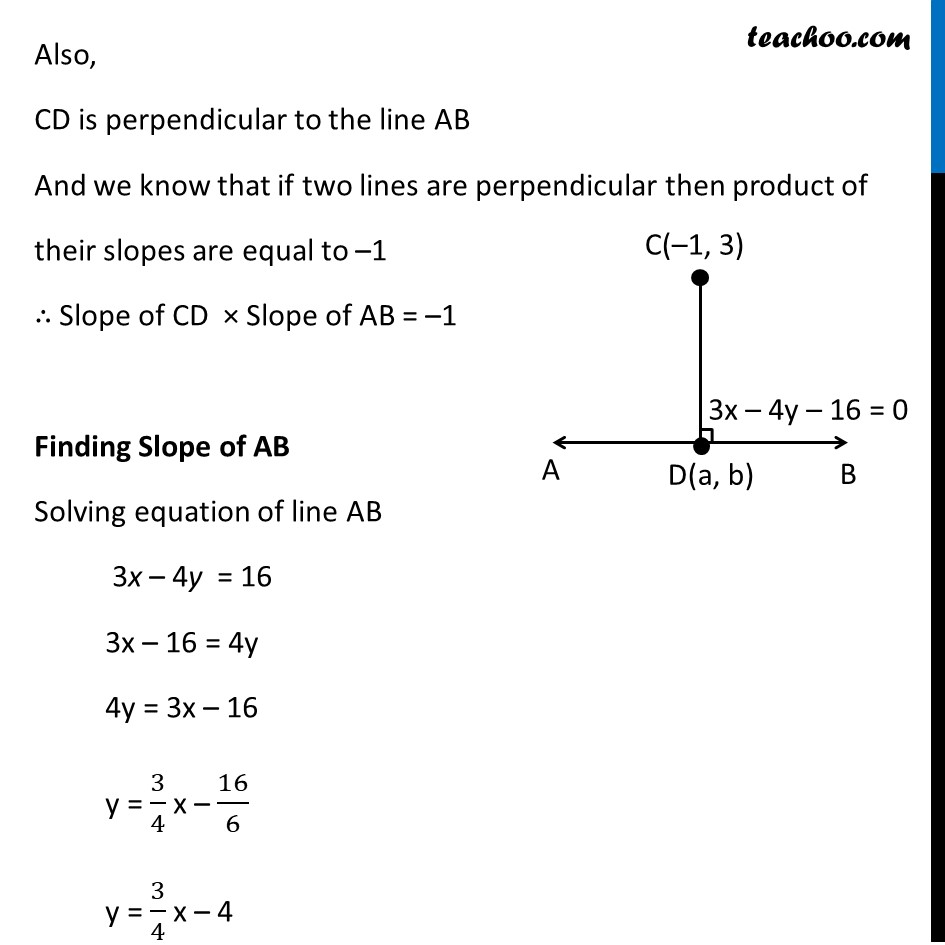
Ex 9.3, 13 Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0. Let the equation of line AB be 3x – 4y – 16 = 0 & Point C be (–1, 3) CD is perpendicular to the line AB & we need to find coordinates of point D Let coordinates of point D be (a, b) Also point D(a, b) lies on the line AB i.e. point (a, b) satisfy the equation of line AB 3x – 4y – 16 = 0 Putting x = a & y = b in equation 3a – 4b – 16 = 0 3a – 4b = 16 Also, CD is perpendicular to the line AB And we know that if two lines are perpendicular then product of their slopes are equal to –1 ∴ Slope of CD × Slope of AB = –1 Finding Slope of AB Solving equation of line AB 3x – 4y = 16 3x – 16 = 4y 4y = 3x – 16 y = 3/4 x – 16/6 y = 3/4 x – 4 The above equation is of the form y = mx + c where m = slope of line ∴ m = 3/4 Slope of line AB = 3/4 Now, Slope of CD × Slope of AB = –1 Slope of CD × 3/4 = –1 Slope of CD = –1 × 4/3 Slope of CD = (−4)/3 Also, Line CD passes through the point C (–1, 3) & D (a, b) So, Slope of CD = (𝑦_2 − 𝑦_1)/(𝑥_2 − 𝑥_1 ) (−4)/3 = (𝑏 − 3)/(𝑎 − (−1)) (−4)/3 = (𝑏 − 3)/(𝑎 + 1) –4(a + 1) = 3 (b – 3) –4a – 4 = 3b – 9 –4a – 3b = –9 + 4 –(4a + 3b) = −5 4a + 3b = 5 Now, our equations are 3a – 4b = 16 4a + 3b = 5 From (2) 4a + 3b = 5 4a = 5 – 3b a = (5 − 3𝑏)/4 Putting value of a in (1) 3a – 4b = 16 3((5 − 3𝑏)/4) – 4b = 16 (3(5 − 3𝑏) − 4𝑏(4))/4 = 16 3(5 – 3b) – 16b = 64 15 – 9b – 16 b = 16 × 4 15 – 25b = 64 – 25b = 64 – 15 –25b = 49 b = 49/(−25) b = (−49)/25 Putting value of b = (−49)/25 in (2) 4a + 3b = 5 4a + 3((−49)/25) = 5 4a – 147/25 = 5 4a = 5 + 147/25 4a = (5(25) + 147)/25 4a = (125 + 147)/25 4a = 272/25 a = 272/(25 × 4) a = 68/25 Hence (a, b) = (68/25, (−49)/25) Hence co-ordinates of point D(a, b) =(𝟔𝟖/𝟐𝟓, (−𝟒𝟗)/𝟐𝟓)