Ex 8.2, 1 - Chapter 8 Class 11 Sequences and Series
Last updated at Dec. 16, 2024 by Teachoo
Geometric Progression(GP): Formulae based
Ex 8.2, 6
You are here
You are here
Chapter 8 Class 11 Sequences and Series
Concept wise
- Finding Sequences
- Arithmetic Progression (AP): Formulae based
- Arithmetic Progression (AP): Statement
- Arithmetic Progression (AP): Calculation based/Proofs
- Inserting AP between two numbers
- Arithmetic Mean (AM)
-
Geometric Progression(GP): Formulae based
- Geometric Progression(GP): Statement
- Geometric Progression(GP): Calculation based/Proofs
- Inserting GP between two numbers
- Geometric Mean (GM)
- AM and GM (Arithmetic Mean And Geometric mean)
- AP and GP mix questions
- Finding sum from series
- Finding sum from nth number
Transcript
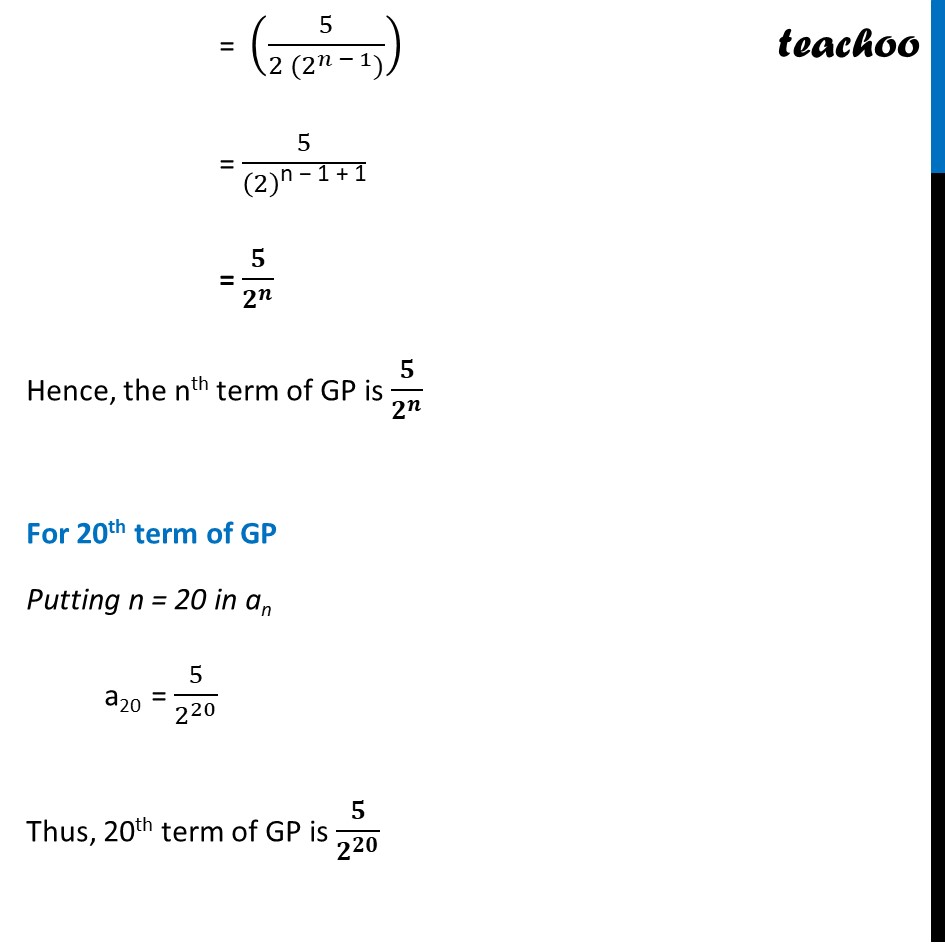
Ex 8.2, 1 Find the 20th and nth terms of the G.P. 5/2, 5/4, 5/8,…. G.P. is 5/2, 5/4, 5/8,…. We know that an = arn – 1 where an = nth term of GP n is the number of terms a is the first term r is the common ratio Here, First term a = 5/2 Common ratio r = (5/4)/(5/2) = 5/4 × 2/5 = 1/2 We need to find nth term, nth term of GP = an = arn-1 Putting a = 5/2 , d = 1/2 = 5/2 (1/2)^(𝑛−1) = 5/2 (1/2^(𝑛−1) ) = (5/(〖2 (2〗^(𝑛−1)))) = 5/(2)"n − 1 + 1" = 5/2^𝑛 Hence, the nth term of GP is 5/2^𝑛 For 20th term of GP Putting n = 20 in an a20 = 5/2^20 Thus, 20th term of GP is 5/2^20
