This question is similar to CBSE Class 12 Sample Paper for 2024 Boards
Please check the question here





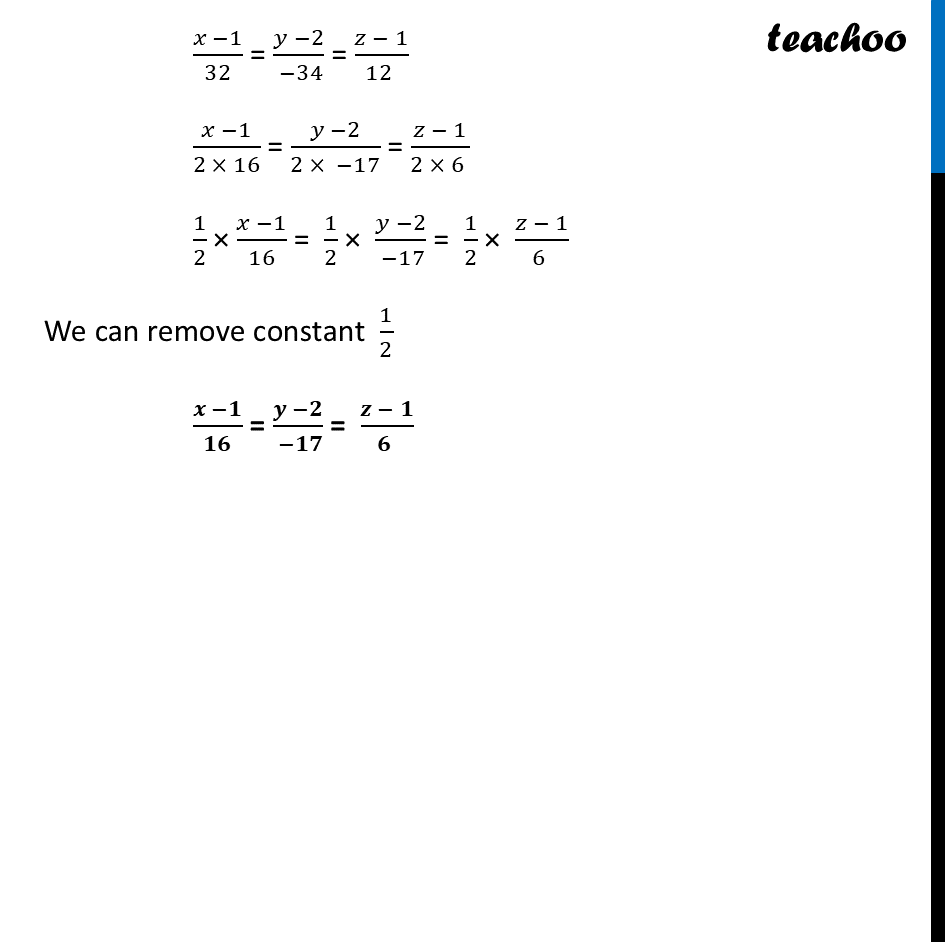
CBSE Class 12 Sample Paper for 2025 Boards
CBSE Class 12 Sample Paper for 2025 Boards
Last updated at February 13, 2025 by Teachoo
This question is similar to CBSE Class 12 Sample Paper for 2024 Boards
Please check the question here








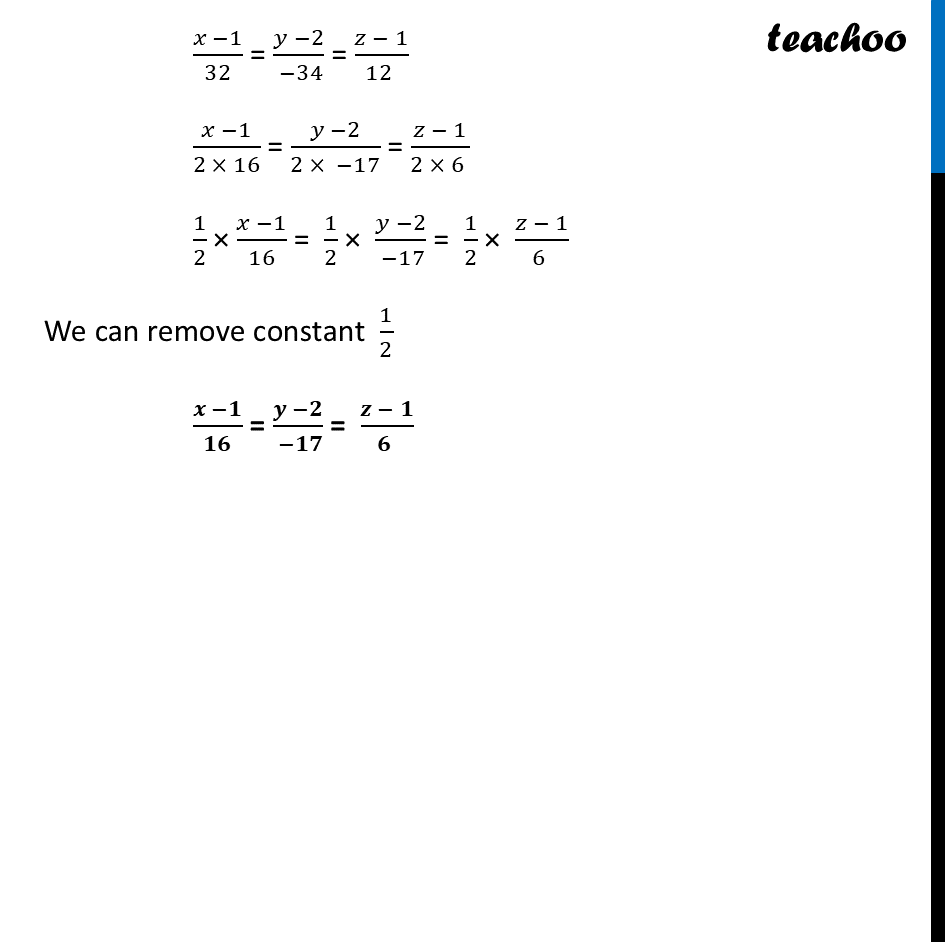
Transcript
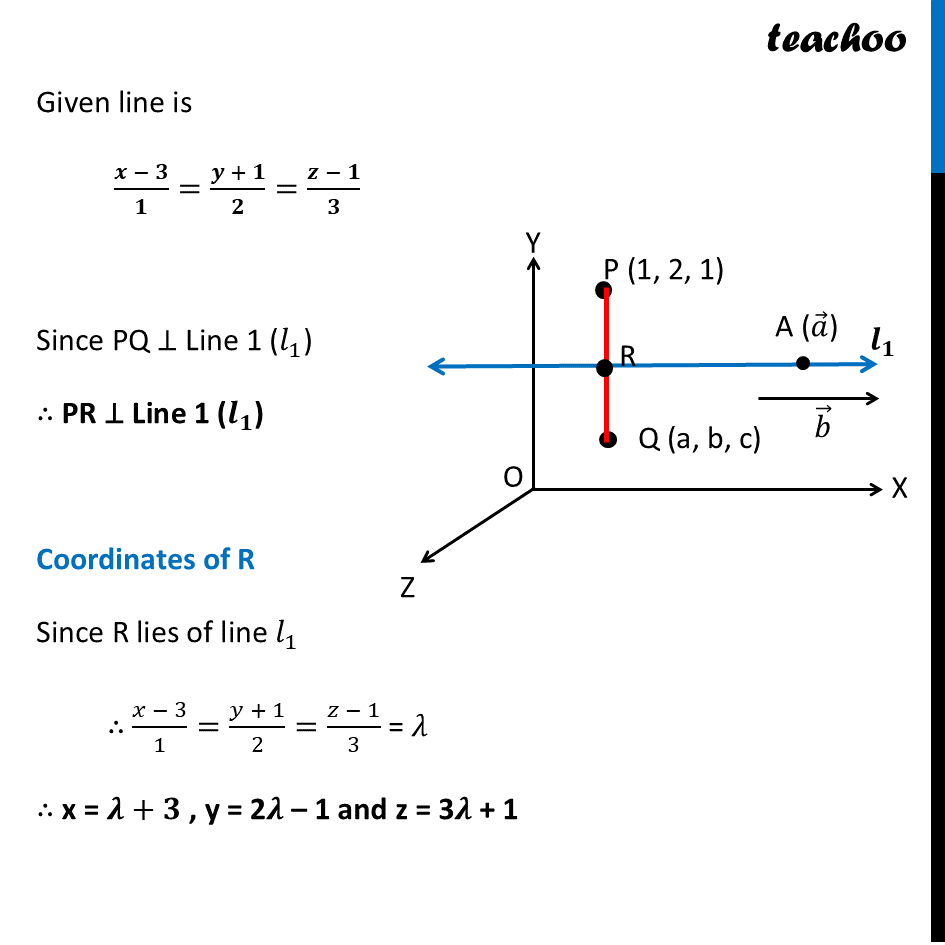
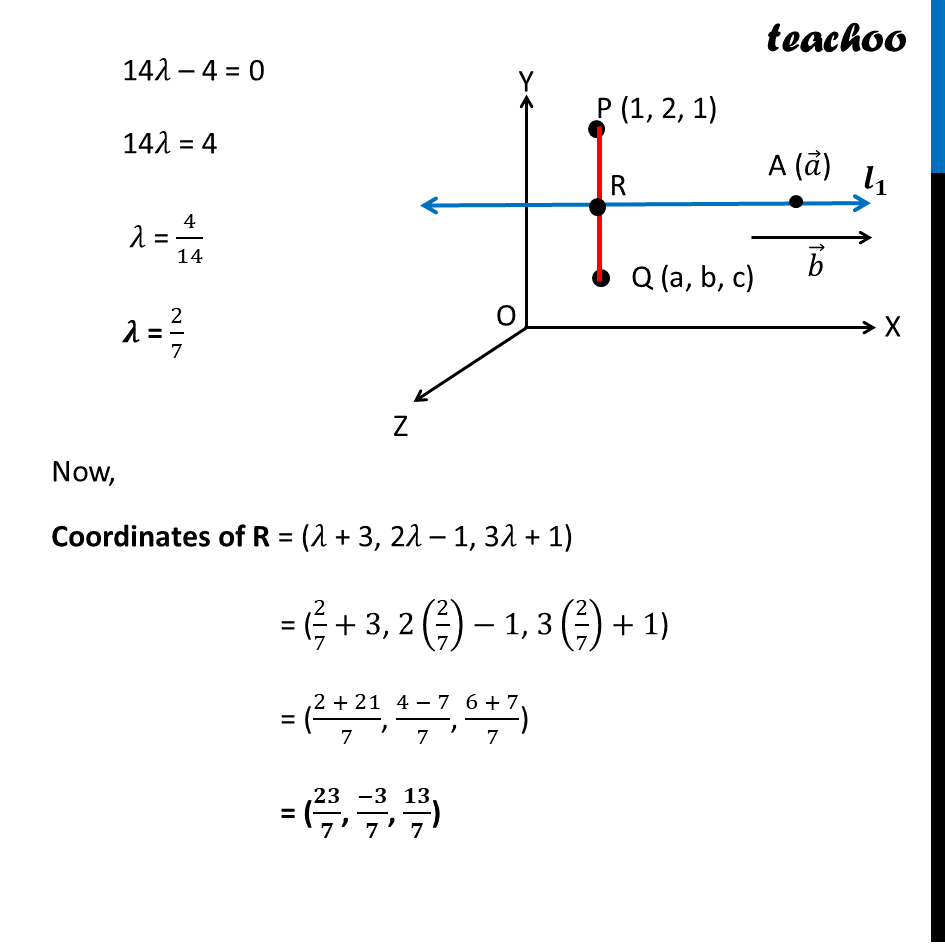
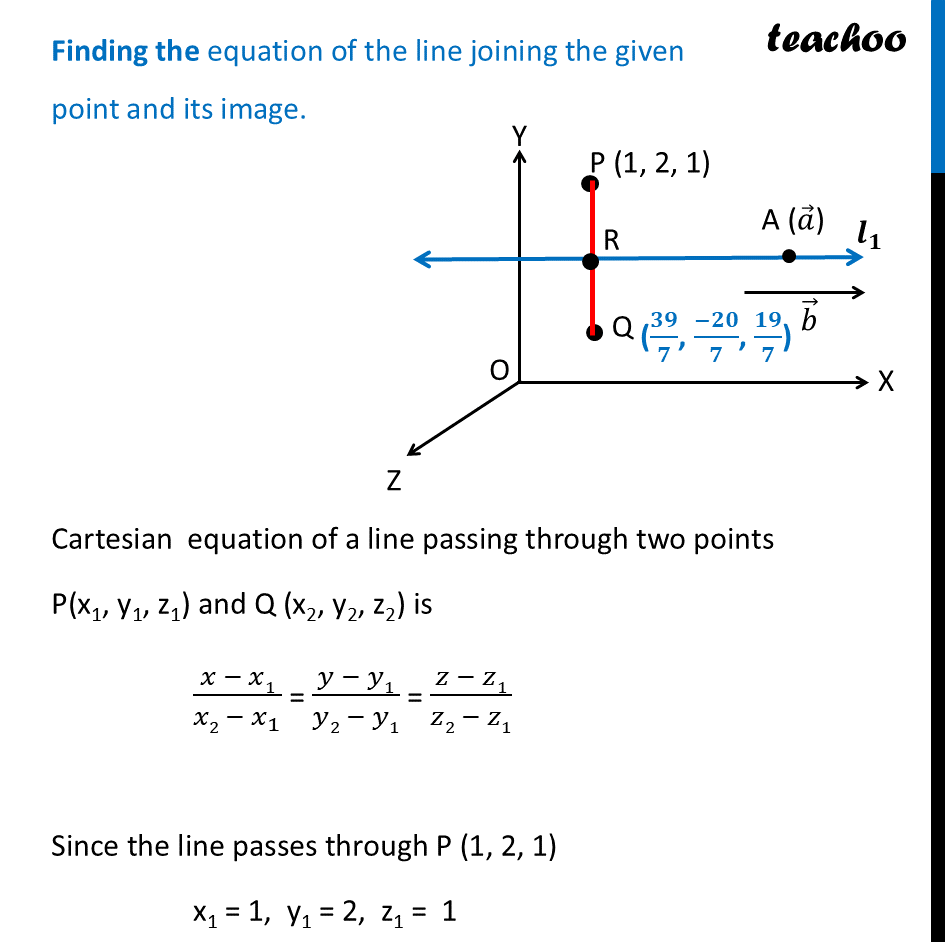
Question 35 (B) Find the image of the point (𝟏,𝟐,𝟏) with respect to the line (𝑥−3)/1=(𝑦+1)/2=(𝑧−1)/3. Also find the equation of the line joining the given point and its image.Let Point P be (1, 2, 1) Let Q (a, b, c) be the image of point P (1, 2, 1) in the line 𝒓 ⃗ Since line is a mirror Point P & Q are at equal distance from line AB, i.e. PR = QR, i.e. R is the mid point of PQ Image is formed perpendicular to mirror i.e. line PQ is perpendicular to line 𝒓 ⃗ Given line is (𝒙 − 𝟑)/𝟏=(𝒚 + 𝟏)/𝟐=(𝒛 − 𝟏)/𝟑 Since PQ ⊥ Line 1 (𝑙_1) ∴ PR ⊥ Line 1 (𝒍_𝟏) Coordinates of R Since R lies of line 𝑙_1 ∴ (𝑥 − 3)/1=(𝑦 + 1)/2=(𝑧 − 1)/3 = 𝜆 ∴ x = 𝝀+𝟑 , y = 2𝝀 – 1 and z = 3𝝀 + 1 So, coordinates of R = (𝝀 + 3, 2𝝀 – 1, 3𝝀 + 1) Now, Since PR ⊥ AB 1(𝝀 + 2) + 2(2𝝀 – 3) + 3 (3𝝀) = 0 𝜆 + 2 + 4𝜆 – 6 + 9𝜆 = 0 Direction ratios of Line 𝒍_𝟏 Since equation of lines is (𝒙 − 𝟑)/𝟏=(𝒚 + 𝟏)/𝟐=(𝒛 − 𝟏)/𝟑 Direction ratios are 1, 2, 3 Direction ratios of Line PR Coordinates of P (1, 2, 1) Coordinates of R (𝜆 + 3, 2𝜆 – 1, 3𝜆 + 1) Direction ratios are 𝜆 + 3 – 1, 2𝜆 – 1 – 2 & 3𝜆 + 1 – 1 i.e. 𝝀 + 2, 2𝝀 – 3 & 3𝝀 14𝜆 – 4 = 0 14𝜆 = 4 𝜆 = 4/14 𝝀 = 2/7 Now, Coordinates of R = (𝜆 + 3, 2𝜆 – 1, 3𝜆 + 1) = (2/7+3, 2(2/7)−1, 3(2/7)+1) = ((2 + 21)/7, (4 − 7)/7, (6 + 7)/7) = (𝟐𝟑/𝟕, (−𝟑)/𝟕, 𝟏𝟑/𝟕) Since R is the midpoint of PQ Coordinates of R = ((𝟏 + 𝒂)/𝟐 " , " (𝟐 + 𝒃)/𝟐 " , " (𝟏 + 𝒄)/𝟐) (𝟐𝟑/𝟕, (−𝟑)/𝟕, 𝟏𝟑/𝟕) = ((𝟏 + 𝒂)/𝟐 " , " (𝟐 + 𝒃)/𝟐 " , " (𝟏 + 𝒄)/𝟐) 𝟐𝟑/𝟕 = (𝟏 + 𝒂)/𝟐 23 × 2 = 7 + 7a 46 = 7 + 7a 46 – 7 = 7a 39 = 7a 7a = 39 a = 𝟑𝟗/𝟕 (−𝟑)/𝟕 = (𝟐 + 𝒃)/𝟐 -3 × 2 = 14 + 7b –6 = 14 + 7b –6 – 14 = 7b –20 = 7b 7b = –20 b = (−𝟐𝟎)/𝟕 𝟏𝟑/𝟕 = (𝟏 + 𝒄)/𝟐 13 × 2 = 7 + 7c 26 = 7 + 7c 26 – 7 = 7c 19 = 7c 7c = 19 c = 𝟏𝟗/𝟕 Hence, Coordinates of Q = (a, b, c) = (𝟑𝟗/𝟕, (−𝟐𝟎)/𝟕, 𝟏𝟗/𝟕) ∴ Q(𝟑𝟗/𝟕, (−𝟐𝟎)/𝟕, 𝟏𝟗/𝟕) is the required image of P Finding the equation of the line joining the given point and its image. Cartesian equation of a line passing through two points P(x1, y1, z1) and Q (x2, y2, z2) is (𝑥 − 𝑥1)/(𝑥2 − 𝑥_1 ) = (𝑦 − 𝑦1)/(𝑦2 − 𝑦1) = (𝑧 − 𝑧1)/(𝑧2 − 𝑧1) Since the line passes through P (1, 2, 1) x1 = 1, y1 = 2, z1 = 1 And also passes through Q (𝟑𝟗/𝟕, (−𝟐𝟎)/𝟕, 𝟏𝟗/𝟕) x2 = 𝟑𝟗/𝟕, y2 = (−𝟐𝟎)/𝟕, z2 = 𝟏𝟗/𝟕 Equation of line is (𝒙 −𝟏)/(𝟑𝟗/𝟕 −𝟏) = (𝒚 −𝟐)/( (−𝟐𝟎)/𝟕 −𝟐) = (𝒛 − 𝟏)/(𝟏𝟗/𝟕 −𝟏) (𝑥 −1)/((39 − 7)/7) = (𝑦 −2)/( (−20 − 14)/7) = (𝑧 − 1)/((19 − 7)/7 ) (𝑥 −1)/(32/7) = (𝑦 −2)/( (−34)/7) = (𝑧 − 1)/(12/7 ) 7 × (𝑥 −1)/32 = 7 × (𝑦 −2)/( −34) = 7 × (𝑧 − 1)/(12 ) We can remove constant 7 (𝑥 −1)/32 = (𝑦 −2)/( −34) = (𝑧 − 1)/(12 ) (𝑥 −1)/(2 × 16) = (𝑦 −2)/(2 × −17) = (𝑧 − 1)/(2 × 6 ) 1/2 × (𝑥 −1)/16 = 1/2 × (𝑦 −2)/( −17) = 1/2 × (𝑧 − 1)/(6 ) We can remove constant 1/2 (𝒙 −𝟏)/𝟏𝟔 = (𝒚 −𝟐)/( −𝟏𝟕) = (𝒛 − 𝟏)/(𝟔 )