CBSE Class 12 Sample Paper for 2025 Boards
You are here
CBSE Class 12 Sample Paper for 2025 Boards
Last updated at Feb. 13, 2025 by Teachoo
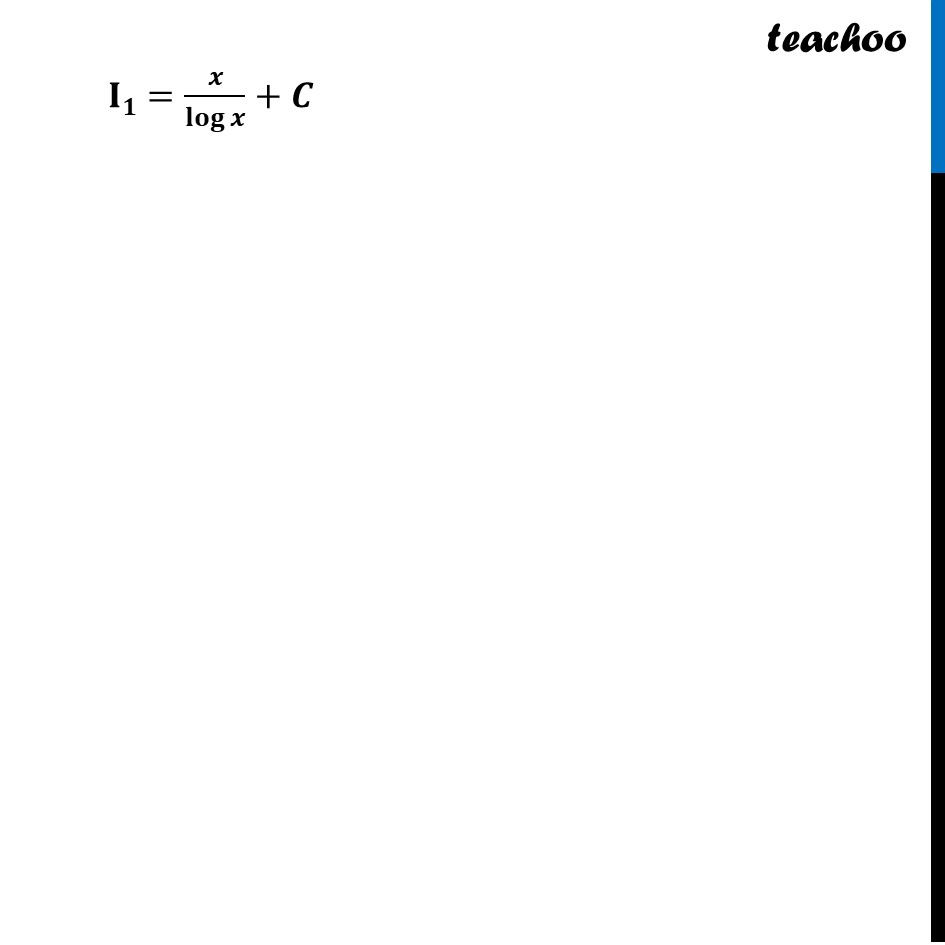
Transcript
Question 29 (A) Evaluate: ∫{1/(log 𝑥)−1/((log 𝑥)^2 )}𝑑𝑥; (where ├ 𝑥>1).Let I1 =∫1▒[1/(log 𝑥)−1/(log𝑥 )^2 ]𝑑𝑥 I1 = ∫1▒〖1/(log 𝑥)−∫1▒〖1/(log𝑥 )^2 .𝑑𝑥〗〗 Solving 𝐈𝟐 I2 =∫1▒𝑙𝑜𝑔(log𝑥 )𝑑𝑥 I2 =∫1▒〖𝑙𝑜𝑔(log𝑥 ).1 𝑑𝑥〗 Using by parts ∫1▒〖𝑓(𝑥) 𝑔(𝑥) 〗 𝑑𝑥=𝑓(𝑥) ∫1▒𝑔(𝑥) 𝑑𝑥−∫1▒(𝑓^′ (𝑥) ∫1▒𝑔(𝑥) 𝑑𝑥) 𝑑𝑥 Putting f(x) = log (log x) and g(x) = 1 I2=1/𝑙𝑜𝑔𝑥 ∫1▒〖1.𝑑𝑥−∫1▒[𝑑(1/𝑙𝑜𝑔𝑥)/𝑑𝑥 ∫1▒〖1.𝑑𝑥〗] 〗 𝑑𝑥 I2=1/𝑙𝑜𝑔𝑥.𝑥−∫1▒〖(−1)/(𝑙𝑜𝑔𝑥)^2 (1/𝑥).𝑥 𝑑𝑥〗 𝐈𝟐=𝒙/𝒍𝒐𝒈𝒙 +∫1▒〖𝟏/(𝒍𝒐𝒈𝒙 )^𝟐 𝒅𝒙〗 Putting the value of I2 in I1 , we get 𝐈𝟏 =𝐈𝟐−∫1▒〖𝟏/(𝒍𝒐𝒈𝒙 )^𝟐 .𝒅𝒙〗 I1 =𝑥/log𝑥 +∫1▒〖1/(log𝑥 )^2 𝑑𝑥〗−∫1▒〖1/(log𝑥 )^2 .𝑑𝑥〗 𝐈𝟏=𝒙/𝐥𝐨𝐠𝒙 +𝑪
