Question 26 - CBSE Class 12 Sample Paper for 2025 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Transcript

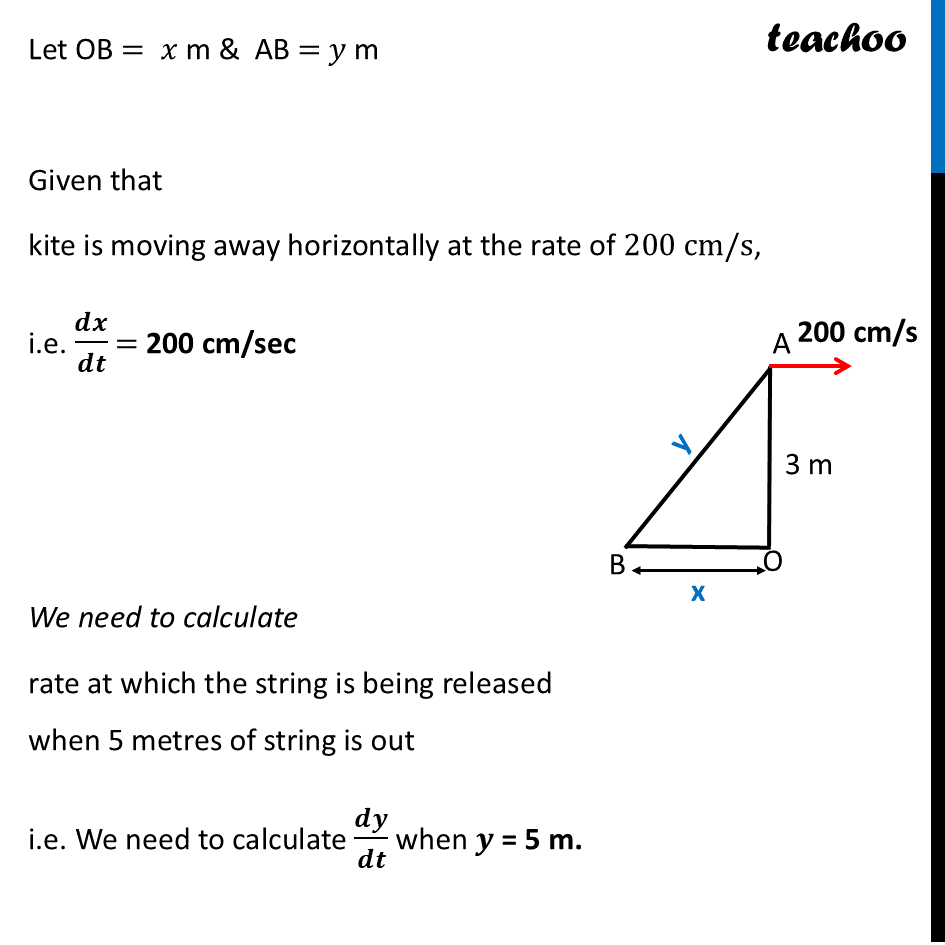
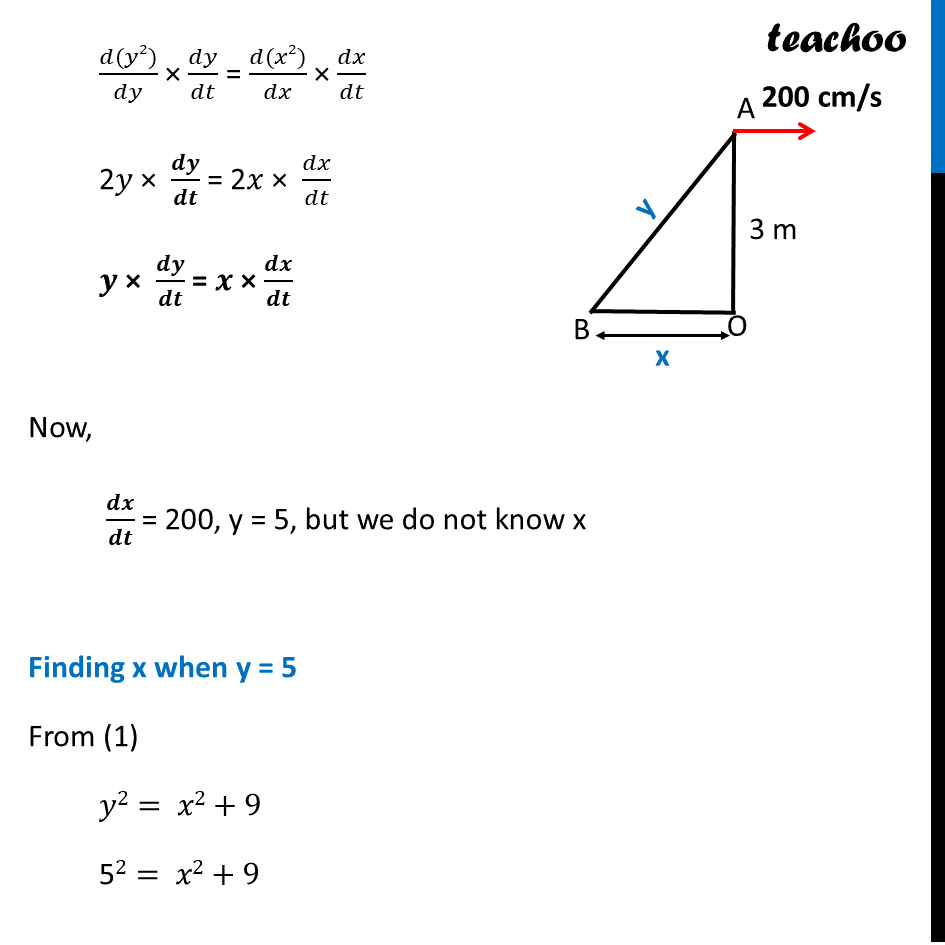
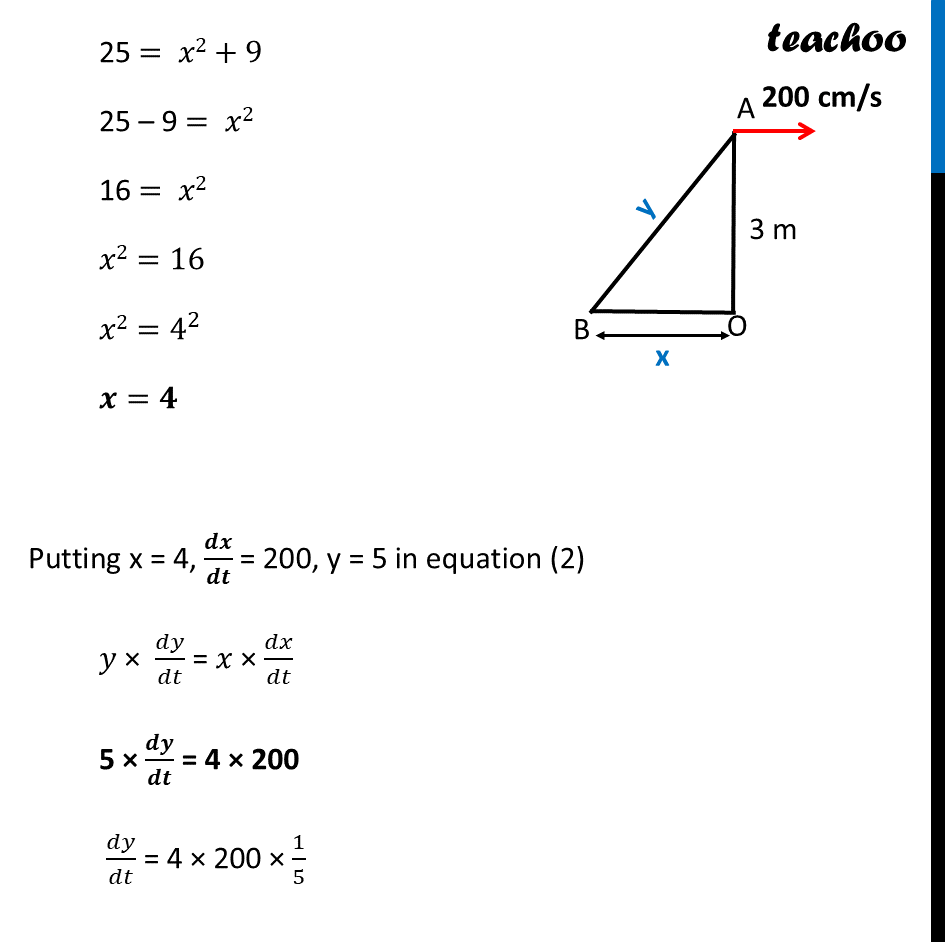
Question 26 A kite is flying at a height of 3 metres and 5 metres of string is out. If the kite is moving away horizontally at the rate of 200" " cm/s, find the rate at which the string is being released.Let AB be the string of kite & OA be the height of kite & OA be the ground. Given Height of kite is 5 m OA = 3 cm Since kite is moving horizontally, Height is fixed, And string length and horizontal distance is variable Let OB = 𝑥 cm & OB = 𝑦 cm Let OB = 𝑥 cm & AB = 𝑦 cm Given that kite is moving away horizontally at the rate of 200" " cm/s, i.e. 𝒅𝒙/𝒅𝒕 = 200 cm/sec We need to calculate rate at which the string is being released when 5 metres of string is out i.e. We need to calculate 𝒅𝒚/𝒅𝒕 when 𝒚 = 5 cm. Since ∆AOB is a right angled triangle Using Pythagoras theorem (AB)2 = (OB)2 + (OA)2 𝑦2= 𝑥2+3^2 𝒚𝟐= 𝒙𝟐+𝟗 Now, Differentiating w.r.t time (𝑑(𝑦2))/𝑑𝑡 =(𝑑(𝑥2))/𝑑𝑡+(𝑑(9))/𝑑𝑡 (𝑑 (𝑦2))/𝑑𝑡 = (𝑑(𝑥2))/𝑑𝑡+0 (𝑑(𝑦2))/𝑑𝑡 × 𝑑𝑦/𝑑𝑦 = (𝑑(𝑥2))/𝑑𝑡 × 𝑑𝑥/𝑑𝑥 (𝑑(𝑦2))/𝑑𝑦 × 𝑑𝑦/𝑑𝑡 = (𝑑(𝑥2))/𝑑𝑥 × 𝑑𝑥/𝑑𝑡 2𝑦 × 𝒅𝒚/𝒅𝒕 = 2𝑥 × 𝑑𝑥/𝑑𝑡 𝒚 × 𝒅𝒚/𝒅𝒕 = 𝒙 × 𝒅𝒙/𝒅𝒕 Now, 𝒅𝒙/𝒅𝒕 = 200, y = 5, but we do not know x Finding x when y = 5 From (1) 𝑦2= 𝑥2+9 52= 𝑥2+9 25 = 𝑥2+9 25 – 9 = 𝑥2 16 = 𝑥2 𝑥2=16 𝑥2=4^2 𝒙=𝟒 Putting x = 4, 𝒅𝒙/𝒅𝒕 = 200, y = 5 in equation (2) 𝑦 × 𝑑𝑦/𝑑𝑡 = 𝑥 × 𝑑𝑥/𝑑𝑡 5 × 𝒅𝒚/𝒅𝒕 = 4 × 200 𝑑𝑦/𝑑𝑡 = 4 × 200 × 1/5 𝑑𝑦/𝑑𝑡 = 4 × 40 𝒅𝒚/𝒅𝒕 = 160 Thus, rate at which the string is being released is 160 cm/s