CBSE Class 12 Sample Paper for 2025 Boards
You are here
CBSE Class 12 Sample Paper for 2025 Boards
Last updated at Feb. 12, 2025 by Teachoo
This question is similar to Chapter 8 Class 12 Application of Integrals - Examples
Please check the question here
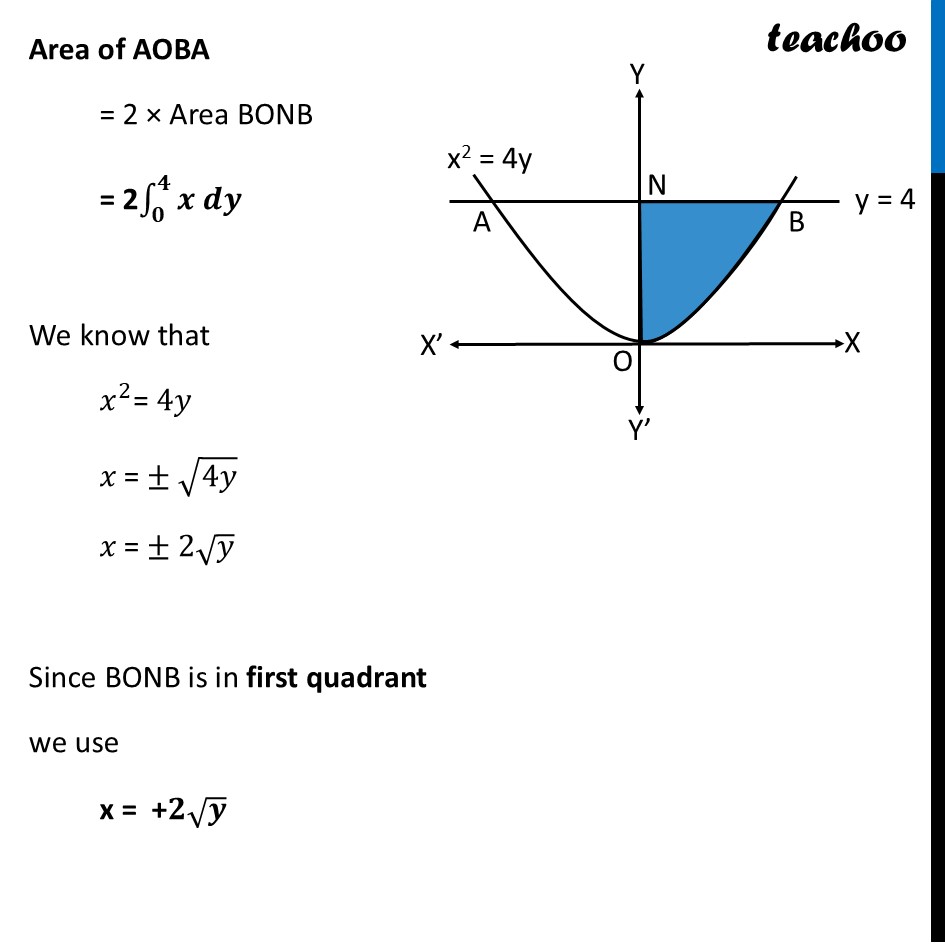
Transcript
Question 18 A student observes an open-air Honeybee nest on the branch of a tree, whose plane figure is parabolic shape given by 𝑥^2=4𝑦. Then the area (in sq units) of the region bounded by parabola 𝑥^2=4𝑦 and the line 𝑦=4 is (A) 32/3 (B) 64/3 (C) 128/3 (D) 256/3Given that y = 4 Let Line AB represent y = 4 Also, Let AOB represent x2 = 4y We have to find area of AOBA Area of AOBA = 2 × Area BONB = 2∫1_𝟎^𝟒▒〖𝒙 𝒅𝒚〗 We know that 𝑥^2= 4𝑦 𝑥 = ± √4𝑦 𝑥 = ± 2√𝑦 Since BONB is in first quadrant we use x = +𝟐√𝒚 Area of AOBA = 2∫1_0^4▒〖𝑥 𝑑𝑦〗 = 2∫1_0^4▒〖2√𝑦 𝑑𝑦〗 = 2 × 2∫1_0^4▒〖〖(𝑦)^(1/2)〗^ 𝑜𝑦〗 = 4 [𝑦^(1/2 + 1)/(1/2 + 1)]_0^4 = 4[𝑦^((1 + 2)/2 )/((1 + 2)/2)]_0^4 = 4[𝑦^(3/2 )/(3/2)]_0^4 = 4 × 2/3 [𝑦^(3/2 ) ]_0^4 = 8/3 〖[(4)〗^(3/2 )−0] = 8/3 [〖(2^2)〗^(3/2 ) ] = 8/3 × 23 = 8/3 × 8 = 𝟔𝟒/𝟑 So, the correct answer is (B)
