Question 33 - Part 2 - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Last updated at Feb. 12, 2025 by Teachoo

This question is similar to Chapter 10 Class 10 Circles - Ex 10.2

Please check the question here

https://www.teachoo.com/1838/539/Ex-10.2--12---A-triangle-ABC-is-drawn-to-circumscribe-a-circle/category/Ex-10.2/

Question 33 - Using above result, find the length BC of 𝛥ABC [Video] - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard

part 2 - Question 33 - Part 2 - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards - Class 10

part 3 - Question 33 - Part 2 - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards - Class 10

Next: Question 34 Important → Share on WhatsApp

Transcript

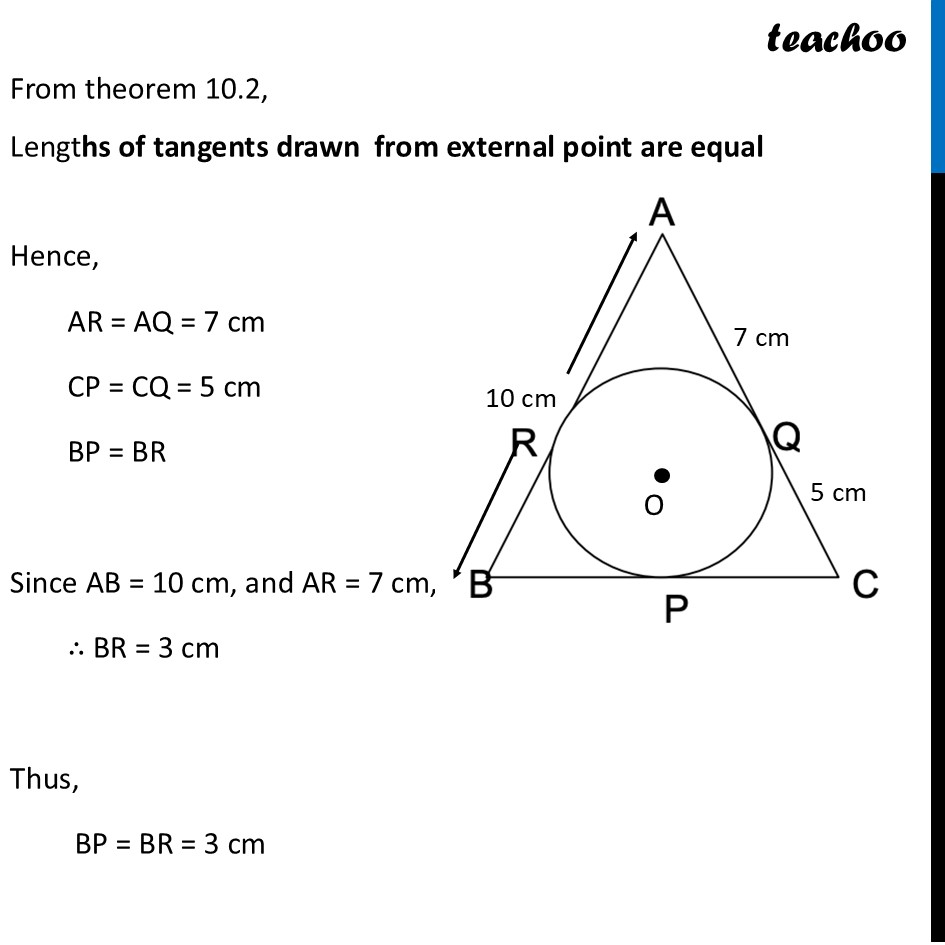
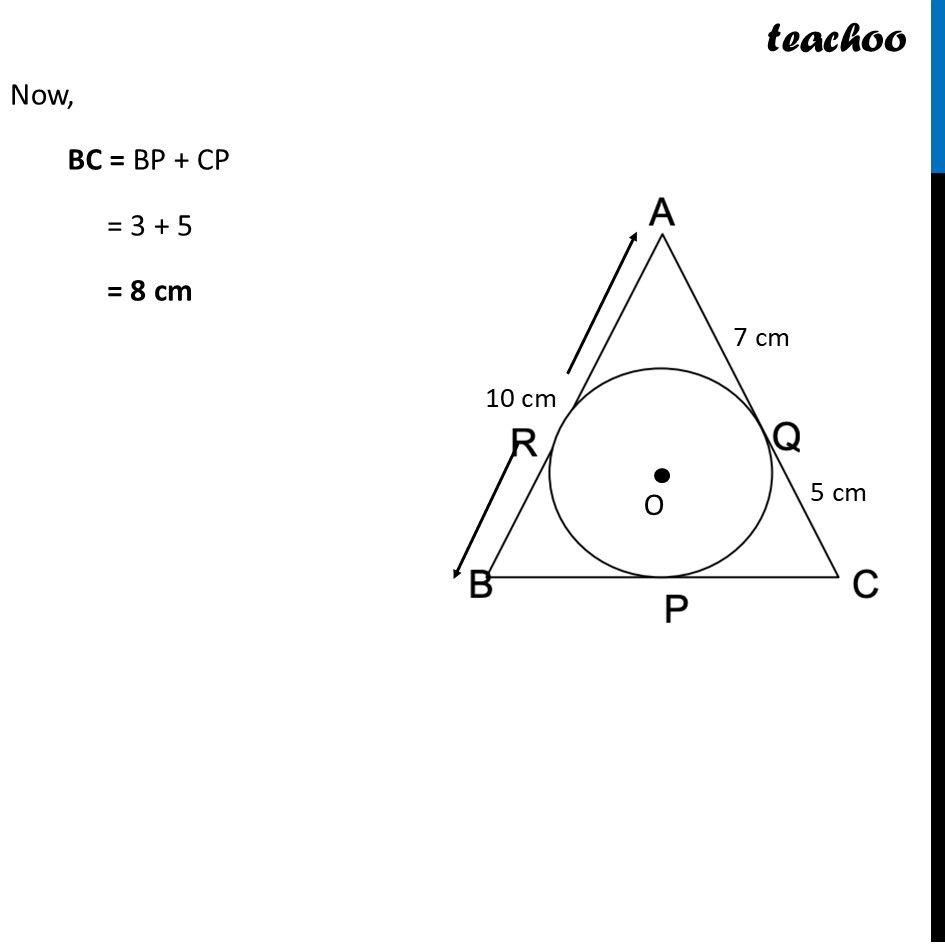
Question 33 – Part 2 Prove that the lengths of tangents drawn from an external point to a circle are equal. Using above result, find the length BC of 𝛥ABC. Given that, a circle is inscribed in 𝛥ABC touching the sides AB, BC and CA at R, P and Q respectively and AB= 10 cm, AQ= 7cm ,CQ= 5cm. From theorem 10.2, Lengths of tangents drawn from external point are equal Hence, AR = AQ = 7 cm CP = CQ = 5 cm BP = BR Since AB = 10 cm, and AR = 7 cm, ∴ BR = 3 cm Thus, BP = BR = 3 cm Now, BC = BP + CP = 3 + 5 = 8 cm

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 15 years. He provides courses for Maths, Science and Computer Science at Teachoo

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular