Question 32 (B) - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Transcript

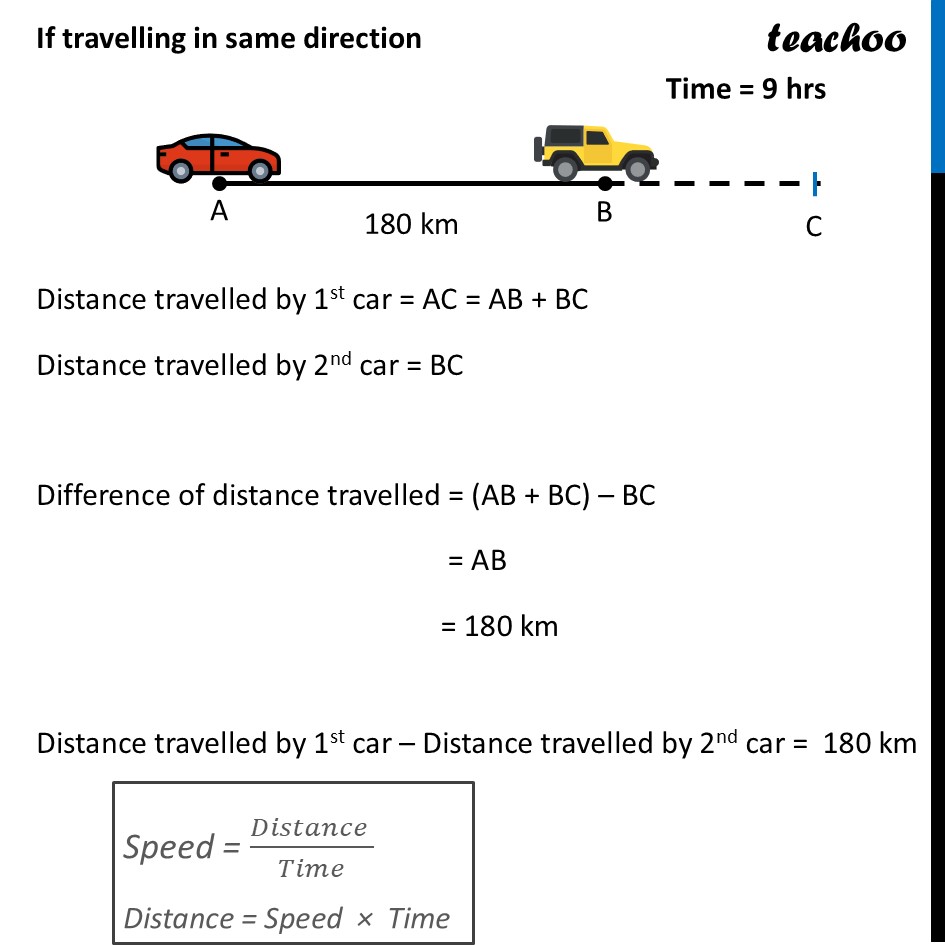
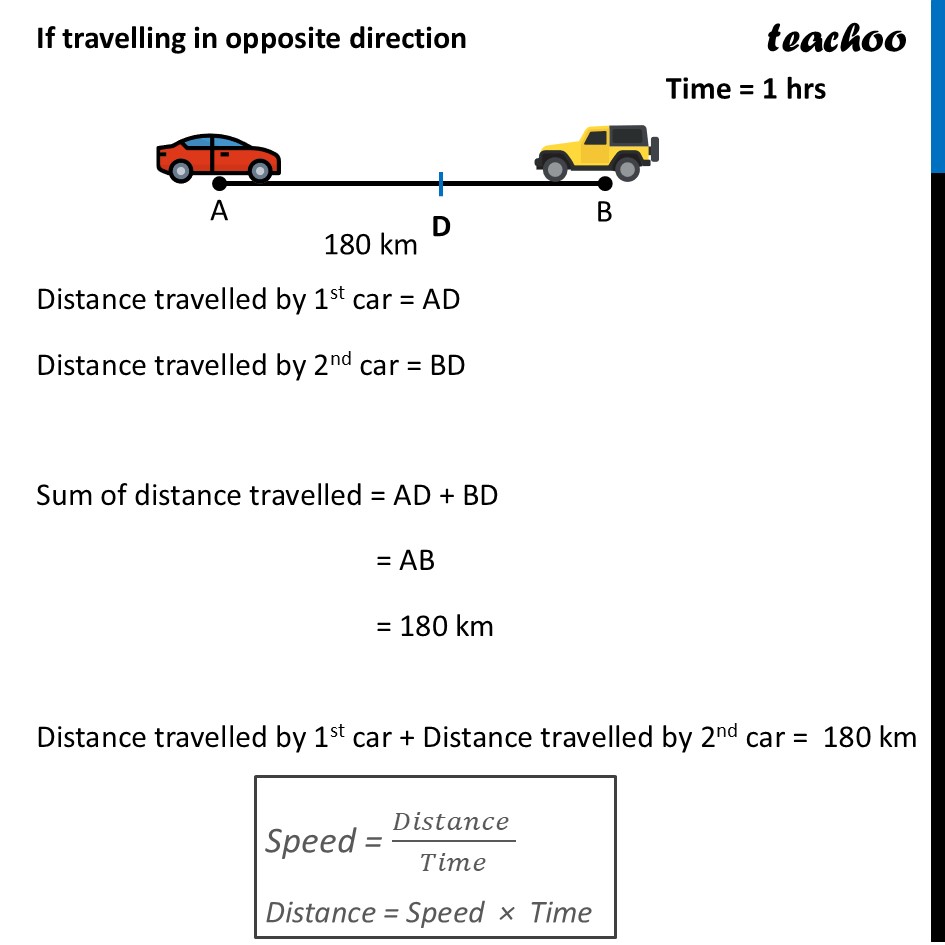
Question 32 (B) Places A and B are 180 km apart on a highway. One car starts from A and another from B at the same time. If the car travels in the same direction at different speeds, they meet in 9 hours. If they travel towards each other with the same speeds as before, they meet in an hour. What are the speeds of the two cars? Let Speed of first car be x km/hr & Speed of second car be y km/hr 180 km If travelling in same direction Distance travelled by 1st car = AC = AB + BC Distance travelled by 2nd car = BC Difference of distance travelled = (AB + BC) – BC = AB = 180 km Distance travelled by 1st car – Distance travelled by 2nd car = 180 km Speed = (𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 )/𝑇𝑖𝑚𝑒 Distance = Speed × Time (Speed of first car × 9 hours) – (Speed of 2nd car × 9 hours) = 180 km 9x – 9y = 180 9(x – y) = 180 (x – y) = 180/9 x – y = 20 If travelling in opposite direction Distance travelled by 1st car = AD Distance travelled by 2nd car = BD Sum of distance travelled = AD + BD = AB = 180 km Distance travelled by 1st car + Distance travelled by 2nd car = 180 km Speed = (𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 )/𝑇𝑖𝑚𝑒 Distance = Speed × Time (Speed of first car × 1 hours) + (Speed of 2nd car × 1 hours) = 100 km x + y = 180 So, our two equations are x – y = 20 …(1) x + y = 180 …(2) From (1) x – y = 20 x = y + 20 Putting value of x in (2) x + y = 180 (y + 20) + y = 180 2y + 20 = 180 2y = 180 – 20 2y = 160 y = 160/2 y = 80 Putting y = 80 in equation (1) x – y = 20 x – 80 = 20 x = 80 + 20 x = 100 Therefore x = 100, y = 80 is the solution Thus, Speed of first car = x km/hr = 100 km/hr Speed of second car = y km/hr = 80 km/hr