CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
You are here
CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
Last updated at Feb. 12, 2025 by Teachoo
This question is similar to Chapter 11 Class 10 Areas related to Circles - Ex 11.1
Please check the Question here
![[Video] AB is a chord of a circle centred at O such that ∠AOB=60 - CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard](https://cdn.teachoo.com/6b0e794a-271b-4470-b46b-2dd2b4b96b33/slide89.jpg)
Transcript
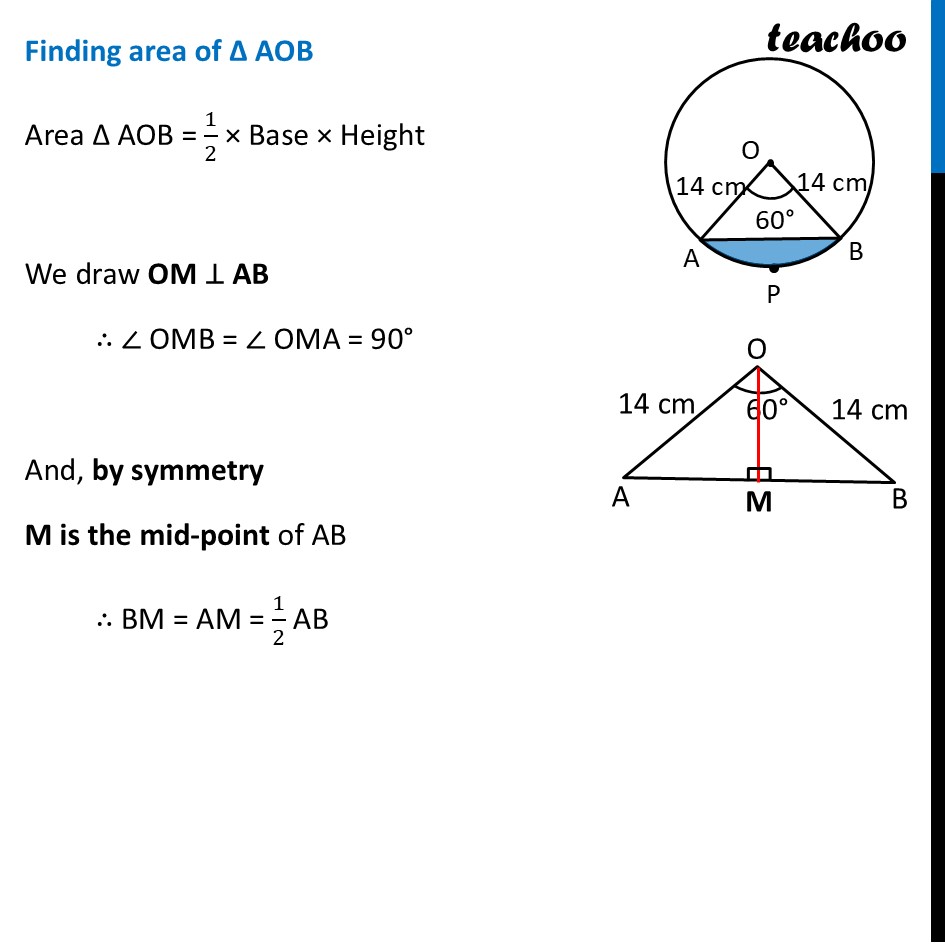
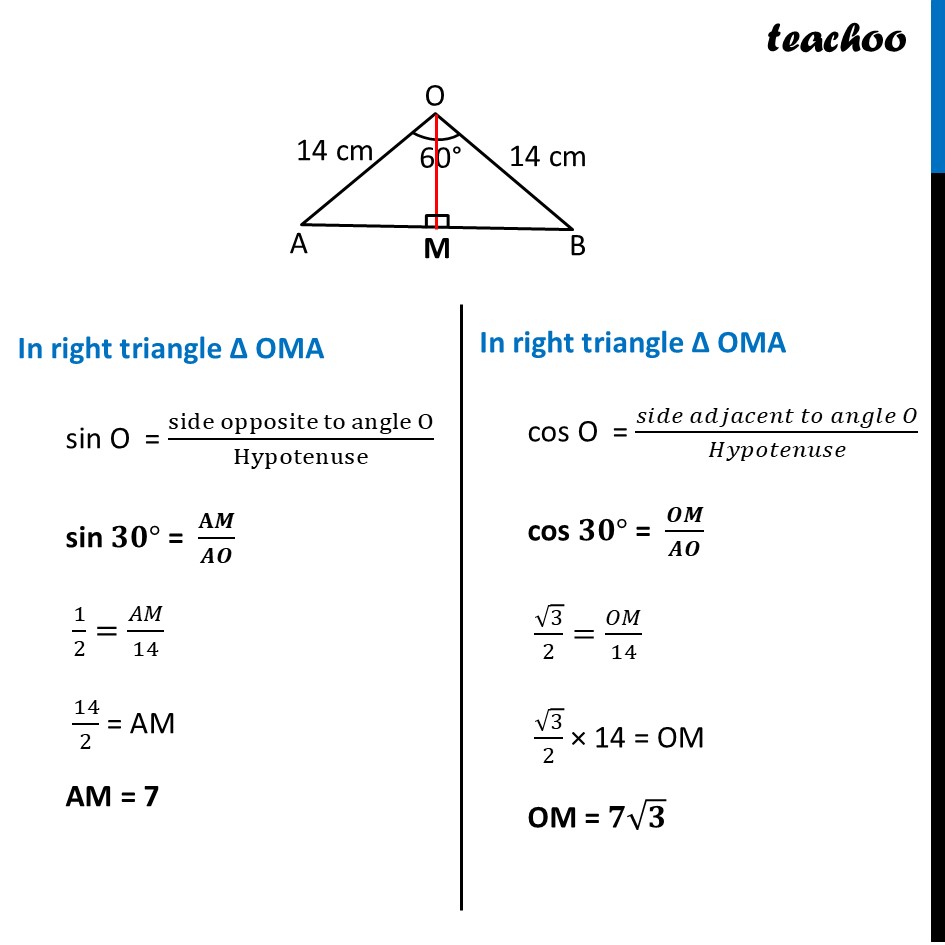
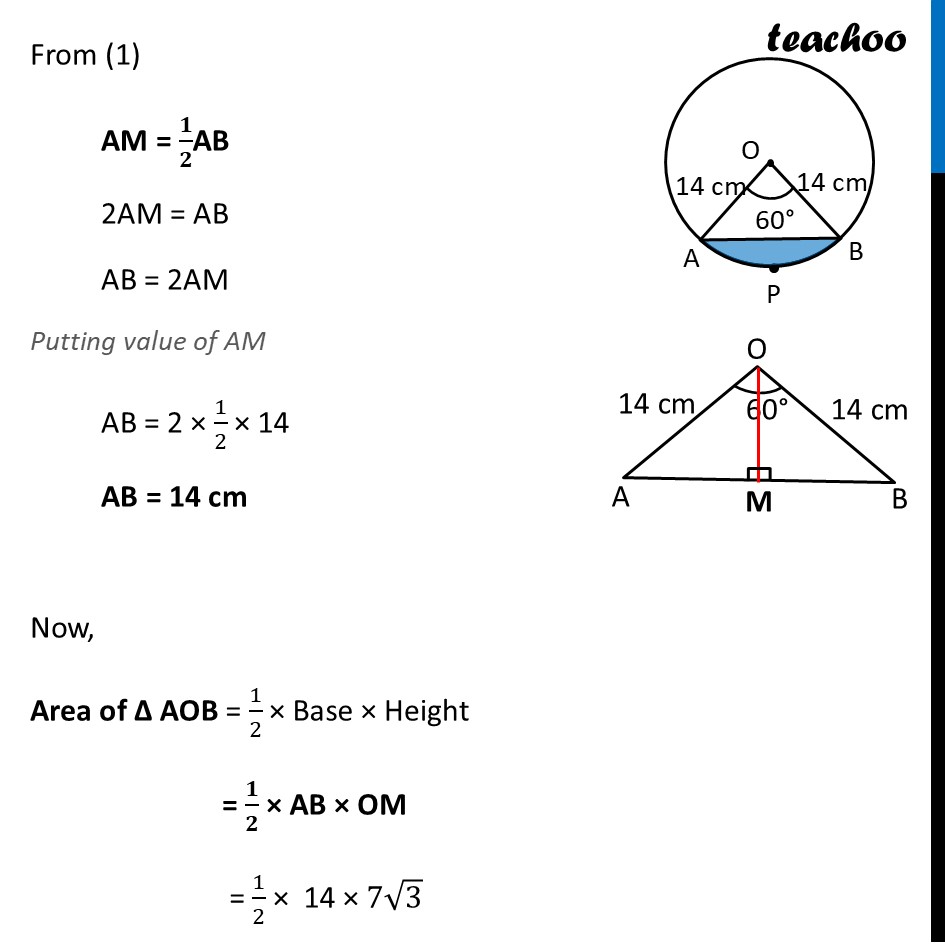
Question 30 (B) AB is a chord of a circle centred at O such that ∠AOB=60˚. If OA = 14 cm then find the area of the minor segment. (take √3 = 1.73)Area of segment APB = Area of sector OAPB – Area of ΔOAB Now, Area of sector OAPB = 𝜃/360×𝜋𝑟2 = 𝟔𝟎/𝟑𝟔𝟎 × 𝟐𝟐/𝟕 × 𝟏𝟒 × 𝟏𝟒 = 1/6 × 22/7 × 14 × 14 = 1/6 × 22 × 2 × 14 = 102.67 cm2 Finding area of Δ AOB Area Δ AOB = 1/2 × Base × Height We draw OM ⊥ AB ∴ ∠ OMB = ∠ OMA = 90° And, by symmetry M is the mid-point of AB ∴ BM = AM = 1/2 AB In right triangle Δ OMA sin O = (side opposite to angle O)/Hypotenuse sin 𝟑𝟎° = 𝐀𝑴/𝑨𝑶 1/2=𝐴𝑀/14 14/2 = AM AM = 7 In right triangle Δ OMA cos O = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑂)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 cos 𝟑𝟎° = 𝑶𝑴/𝑨𝑶 √3/2=𝑂𝑀/14 √3/2 × 14 = OM OM = 𝟕√𝟑 From (1) AM = 𝟏/𝟐AB 2AM = AB AB = 2AM Putting value of AM AB = 2 × 1/2 × 14 AB = 14 cm Now, Area of Δ AOB = 1/2 × Base × Height = 𝟏/𝟐 × AB × OM = 1/2 × 14 × 7√3 = 𝟒𝟗√𝟑 cm2 = 49 × 1.73 = 84.77 cm2 Therefore, Area of segment APB = Area of sector OAPB – Area of ΔOAB = 102.67 − 84.77 = 17.9 cm2
