Question 4 - Coefficient - Chapter 7 Class 11 Binomial Theorem

Transcript

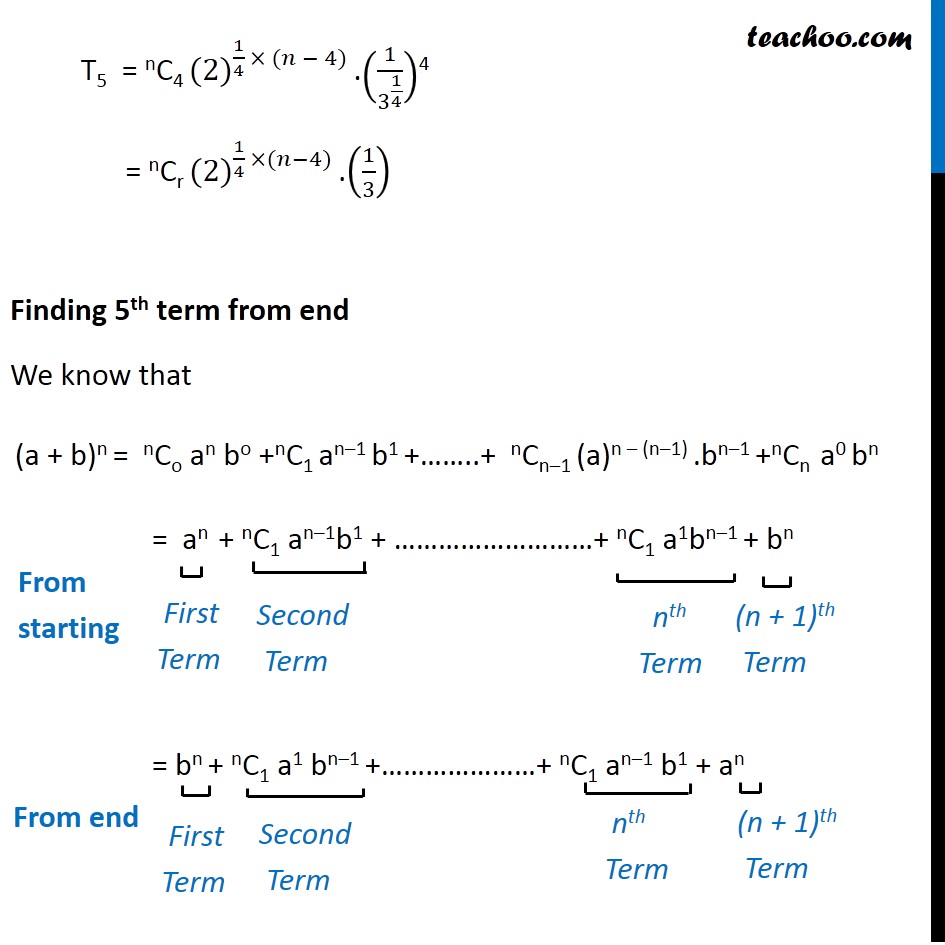
Question 4 Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of (∜2+ 1/∜3)^𝑛 is √6 : 1 We know that General term of expansion (a + b)n Tr + 1 = nCr an – rbr Fifth term from beginning We need to calculate T5 = T4 + 1 Putting r = 4 , a = ∜2 , b = (1/∜3) T4 + 1 = nC4(∜2)n – 4.(1/∜3)4 T5 = nC4 〖((2)〗^(1/4))n – 4 .(1/3^(1/4) )4 T5 = nC4 〖(2)〗^(1/4 × (𝑛 − 4)) .(1/3^(1/4) )4 = nCr 〖(2)〗^(1/4 ×(𝑛−4)) .(1/3) Finding 5th term from end We know that (a + b)n = nCo an bo +nC1 an–1 b1 +……..+ nCn–1 (a)n – (n–1) .bn–1 +nCn a0 bn = an + nC1 an–1b1 + ………………………+ nC1 a1bn–1 + bn = bn + nC1 a1 bn–1 +…………………+ nC1 an–1 b1 + an Hence, 5th term from end = (n – 3)th term from beginning Another method, rth term from end = (n – r + 2)th term from stating 5th term from end = (n – 5 + 2)th term from stating = (n – 3)th term from beginning Now we need to calculate (n – 3)th term of expansion (√(𝟒&𝟐) + 𝟏/√(𝟒&𝟑) )r Tr + 1 = nCr an – rbr Putting r = (n – 3) – 1 = n – 4 a = ∜2 , b = 1/∜3 T(n – 4 + 1) = nCn – 4 (∜2)^(𝑛 −(𝑛−4)) . (1/∜3)^(𝑛 − 4) = nCn – 4 [〖(2)〗^(1/4) ]^"n – n + 4" . (1/3^(1/4) )^(𝑛 − 4) = nCn – 4 [〖(2)〗^(1/4) ]^"4" . (3^((−1)/4) )^(𝑛 − 4) = nCn – 4 〖(2)〗^1 .(1/3)^((𝑛 − 4)/4) = nCn – 4 〖(2)〗^(4/4) .3^((−(𝑛 − 4))/4) = nCn – 4 〖(2)〗^1 .(1/3)^((𝑛 − 4)/4) Given that Ratio fifth term from beginning fifth term from end is √6 : 1 (𝐹𝑖𝑓𝑡ℎ 𝑡𝑒𝑟𝑚 𝑓𝑟𝑜𝑚 𝑏𝑒𝑔𝑖𝑛𝑛𝑖𝑛𝑔 )/(𝐹𝑖𝑓𝑡ℎ 𝑡𝑒𝑟𝑚 𝑓𝑟𝑜𝑚 𝑒𝑛𝑑 ) = √6/1 (〖𝑛𝐶〗_4 2^((𝑛−4)/4) . 1/3)/(〖𝑛𝐶〗_(𝑛−4) 2 . (1/3)^((𝑛−4)/4) ) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ) . (2)^((𝑛 − 4)/4 −1 ) (1/3)^( 1 − ((𝑛 − 4)/4) ) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ) . 2^((𝑛 − 4 − 4)/4 ). (1/3)^((4 − 𝑛 + 4)/4) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ). 2^((𝑛 − 8)/4 ). (1/3)^((8 − 𝑛)/4) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ). 2^((𝑛 − 8)/4 ). (1/3)^((−(𝑛 − 8))/4) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ). 2^((𝑛−8)/4). (3)^((𝑛 − 8)/4) = √6/1 (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ). 〖(2 × 3)〗^((𝑛 − 8)/4). = 6^(1/2) (〖𝑛𝐶〗_4 )/(〖𝑛𝐶〗_(𝑛−4) ). 6^((𝑛 − 8)/4)= 6^(1/2) Comparing powers of 6 (𝑛 − 8)/4 = 1/2 n – 8 = 4/2 n – 8 = 2 n = 2 + 8 n = 10 Hence, n = 10