



Examples
Last updated at Dec. 16, 2024 by Teachoo





Transcript
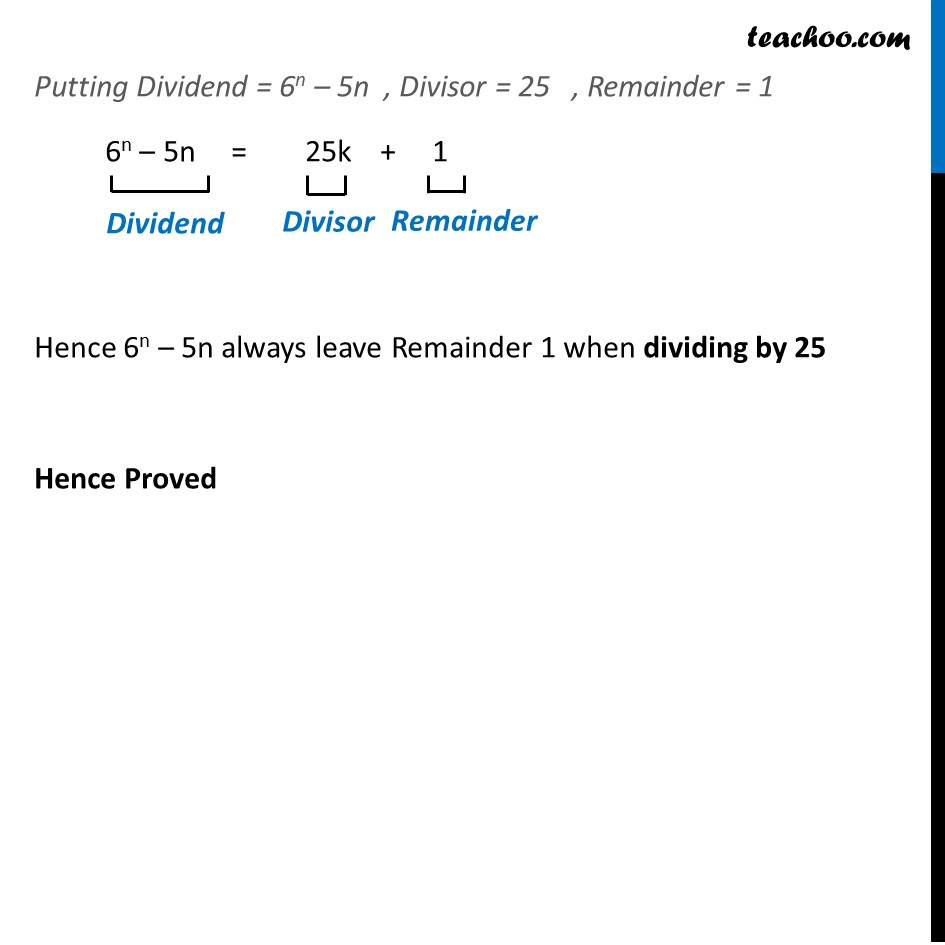
Example 4 Using binomial theorem, prove that 6n – 5n always leaves remainder 1 when divided by 25. Writing 6n = (1 + 5)n (6)n = nC0 1n 50 + nC1 1n – 1 51 + nC2 1n – 2 52…... + nCn 1n – n 5n = nC0 50 + nC1 51 + nC2 52 + ………..…... + nCn 5n = 1 × 1 + 𝑛!/1!( 𝑛 −1)! 51 + 𝑛!/2!( 𝑛 −2)! 52 +………. + 1 × 5n = 1 + (𝑛(𝑛−1)!)/1( 𝑛−1)! 5 + (𝑛(𝑛 − 1)(𝑛 − 2)!)/2( 𝑛 −2)! 52 +………. + 5n = 1 + n(5) + (𝑛(𝑛 − 1) )/2 52 +………. + 5n We know that (a + b)n = nC0 an + nC1 an – 1 b 1 + nC2 an – 2 b2 + ….. + nCn bn Putting a = 1 ,b = 5 Thus, (6)n = 1 + 5n + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + 52 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25k where k = ( (𝑛(𝑛 − 1) )/2 ………. + 5n – 2 ) The above equation is of the form Dividend = Divisor × Quotient + Remainder Thus, (6)n = 1 + 5n + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + 52 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25k where k = ( (𝑛(𝑛 − 1) )/2 ………. + 5n – 2 ) The above equation is of the form Dividend = Divisor × Quotient + Remainder Thus, (6)n = 1 + 5n + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + 52 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25k where k = ( (𝑛(𝑛 − 1) )/2 ………. + 5n – 2 ) The above equation is of the form Dividend = Divisor × Quotient + Remainder Putting Dividend = 6n – 5n , Divisor = 25 , Remainder = 1 6n – 5n = 25k + 1 Hence 6n – 5n always leave Remainder 1 when dividing by 25 Hence Proved Example 4 Using binomial theorem, prove that 6n – 5n always leaves remainder 1 when divided by 25. Writing 6n = (1 + 5)n (6)n = nC0 1n 50 + nC1 1n – 1 51 + nC2 1n – 2 52…... + nCn 1n – n 5n = nC0 50 + nC1 51 + nC2 52 + ………..…... + nCn 5n = 1 × 1 + 𝑛!/1!( 𝑛 −1)! 51 + 𝑛!/2!( 𝑛 −2)! 52 +………. + 1 × 5n = 1 + (𝑛(𝑛−1)!)/1( 𝑛−1)! 5 + (𝑛(𝑛 − 1)(𝑛 − 2)!)/2( 𝑛 −2)! 52 +………. + 5n = 1 + n(5) + (𝑛(𝑛 − 1) )/2 52 +………. + 5n We know that (a + b)n = nC0 an + nC1 an – 1 b 1 + nC2 an – 2 b2 + ….. + nCn bn Putting a = 1 ,b = 5 Thus, (6)n = 1 + 5n + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + (𝑛(𝑛 − 1) )/2 52………. + 5n 6n – 5n = 1 + 52 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25 ((𝑛(𝑛 − 1) )/2 " ………. + 5n – 2" ) 6n – 5n = 1 + 25k where k = ( (𝑛(𝑛 − 1) )/2 ………. + 5n – 2 ) The above equation is of the form Dividend = Divisor × Quotient + Remainder Putting Dividend = 6n – 5n , Divisor = 25 , Remainder = 1 6n – 5n = 25k + 1 Hence 6n – 5n always leave Remainder 1 when dividing by 25 Hence Proved