Question 9 - Coefficient - Chapter 7 Class 11 Binomial Theorem

Transcript

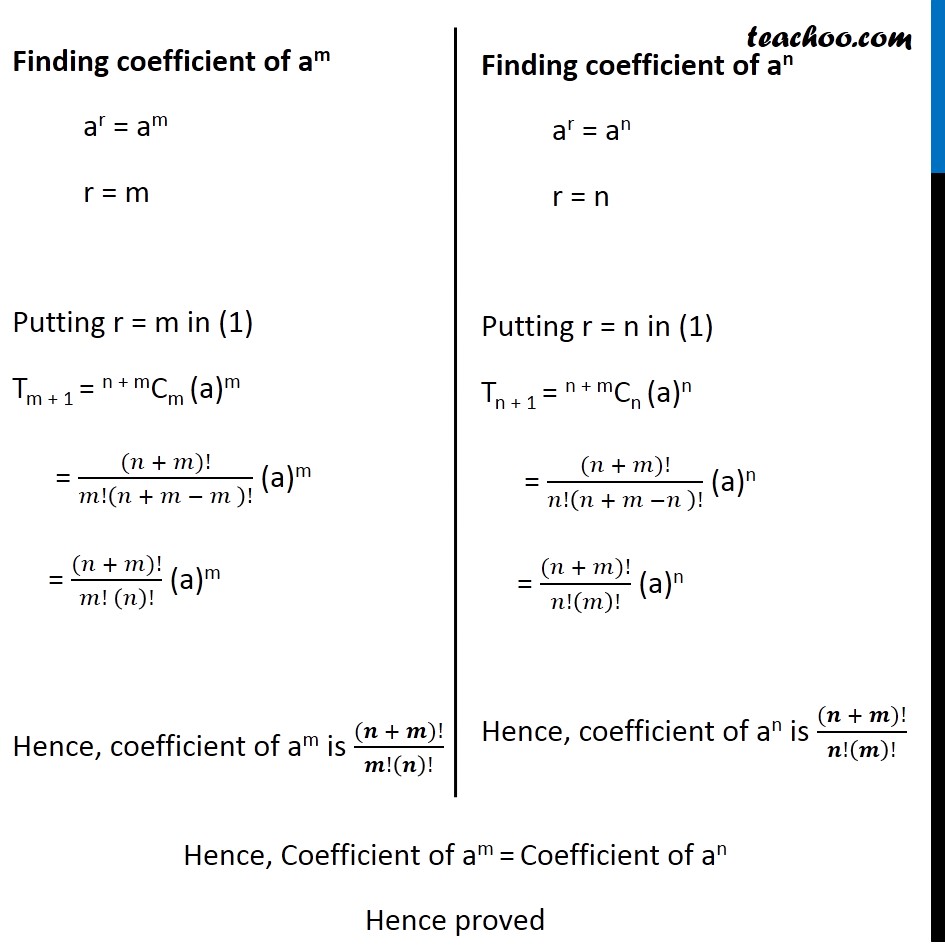
Question 9 In the expansion of (1 + a)m + n, prove that coefficients of am and an are equal. We know that General term of expansion (a + b)n is Tr+1 = nCr an–r br For (1 + a)m + n, Putting n = m + n , a = 1, b = a Tr+1 = n + mCr (1)n + m – r (a)r = n + mCr (a)r Finding coefficient of am ar = am r = m Putting r = m in (1) Tm + 1 = n + mCm (a)m = ((𝑛 + 𝑚)!)/𝑚!(𝑛 + 𝑚 − 𝑚 )! (a)m = ((𝑛 + 𝑚)!)/(𝑚! (𝑛)!) (a)m Hence, coefficient of am is ((𝒏 + 𝒎)!)/𝒎!(𝒏)! Finding coefficient of an ar = an r = n Putting r = n in (1) Tn + 1 = n + mCn (a)n = ((𝑛 + 𝑚)!)/𝑛!(𝑛 + 𝑚 −𝑛 )! (a)n = ((𝑛 + 𝑚)!)/𝑛!(𝑚)! (a)n Hence, coefficient of an is ((𝒏 + 𝒎)!)/𝒏!(𝒎)! Hence, Coefficient of am = Coefficient of an Hence proved