











Miscellaneous
Last updated at December 16, 2024 by Teachoo














Transcript
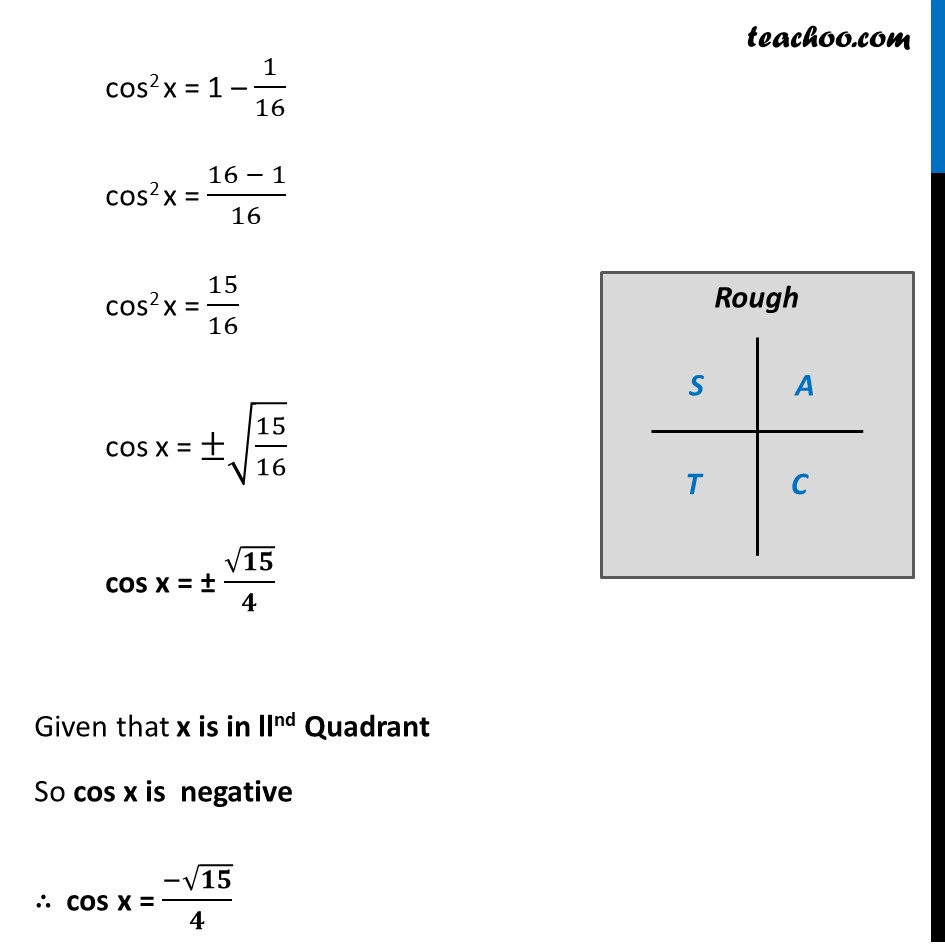
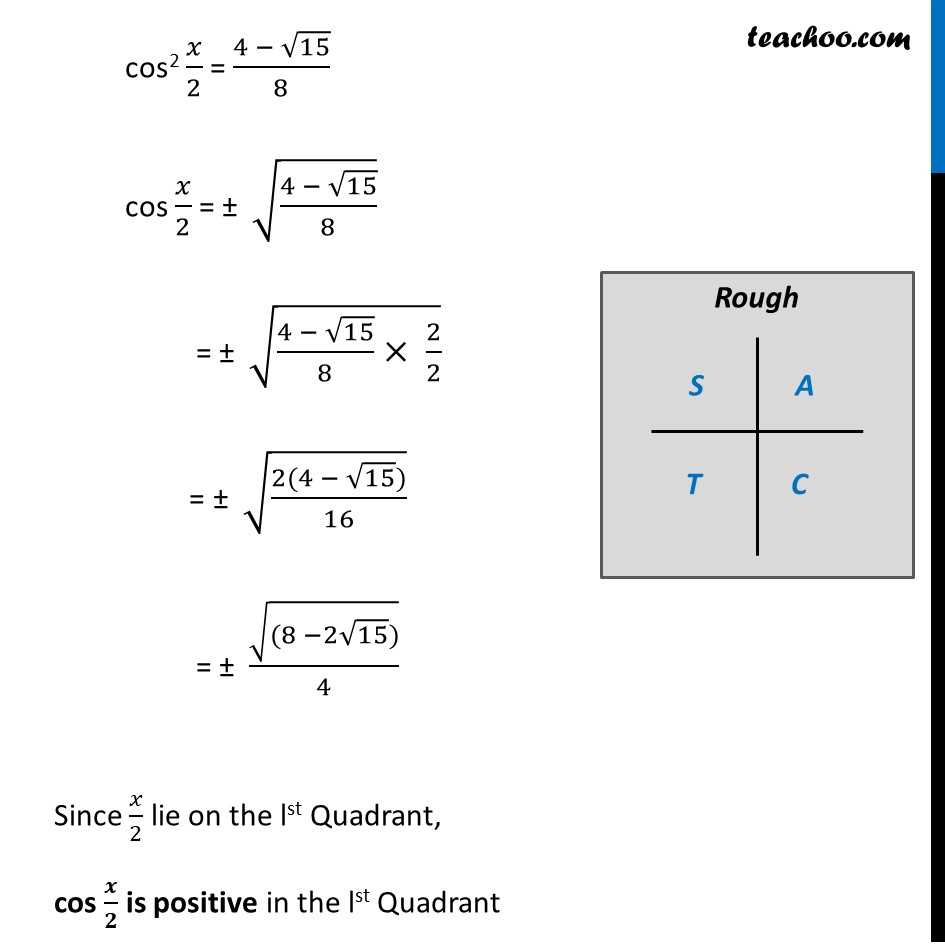
Misc 10 Find sin 𝑥/2, cos 𝑥/2 and tan 𝑥/2 for sin𝑥 = 1/4 , 𝑥 in quadrant II Given that x is in Quadrant II So, 90° < x < 180° Replacing x with 𝑥/2 (90°)/2 < 𝑥/2 < (180°)/2 45° < 𝒙/𝟐 < 90° So, 𝒙/𝟐 lies in Ist quadrant In Ist quadrant, sin , cos & tan are positive sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 are positive Given sin x = 1/4 2 sin 𝒙/𝟐 cos 𝒙/𝟐 = 𝟏/𝟒 sin 𝑥/2 cos 𝑥/2 = 1/4 × 1/2 sin 𝒙/𝟐 cos 𝒙/𝟐 = 𝟏/𝟖 We are given sin x , lets first calculate cos x We know that sin2 x + cos2 x = 1 (1/4)^2 + cos2 x = 1 1/16 + cos2 x = 1 cos2 x = 1 – 1/16 cos2 x = (16 − 1)/16 cos2 x = 15/16 cos x = ±√(15/16) cos x = ± √𝟏𝟓/𝟒 Given that x is in llnd Quadrant So cos x is negative ∴ cos x = (−√𝟏𝟓)/𝟒 We know that cos 2x = 2cos2 x – 1 Replacing x by 𝑥/2 cos x = 2 cos2 𝑥/2 – 1 2cos2 𝑥/2 – 1 = −√15/4 2cos2 𝑥/2 = (4 − √15)/4 cos2 𝑥/2 = (4 − √15)/4 × 1/2 cos2 𝑥/2 = (4 − √15)/(4 × 2) cos2 𝑥/2 = (4 − √15)/8 cos 𝑥/2 = ± √((4 − √15)/8) = ± √((4 − √15)/8× 2/2) = ± √((2(4 − √15))/16) = ± √((8 −2√15))/4 Since 𝑥/2 lie on the lst Quadrant, cos 𝒙/𝟐 is positive in the lst Quadrant So, cos 𝑥/2 = √((8 −2√15))/4 So, cos 𝒙/𝟐 = √((𝟖 −𝟐√𝟏𝟓))/𝟒 Also, from (1) sin 𝑥/2 cos 𝑥/2 = 1/8 Putting value of cos 𝑥/2 "sin " 𝑥/2 × √((8 −2√15))/4 = 1/8 "sin " 𝑥/2 = 1/8 × 4/√((8 −2√15)) "sin " 𝑥/2 = 1/2 × 1/√((8 −2√15)) "sin " 𝑥/2 = 1/2 × 1/√((8 −2√15) × ((8 + 2√15))/((8 + 2√15) )) "sin " 𝑥/2 = 1/2 × 1/√( ((8 −2√15) × (8 + 2√15))/((8 + 2√15) )) "sin " 𝑥/2 × √((8 −2√15))/4 = 1/8 "sin " 𝑥/2 = 1/8 × 4/√((8 −2√15)) "sin " 𝒙/𝟐 = 1/2 × 1/√((8 −2√15)) = 1/2 × √(((8 + 2√15))/((64 − (2)2 (√15)2 )) = 1/2 × √(((8 + 2√15))/((64 − 4 × 15) )) = 1/2 × √(((8 + 2√15))/((64 − 4 × 15) )) = 1/2 × √(((8 + 2√15))/((64 − 60) )) = 1/2 × √(((8 + 2√15))/4) = 1/2 × √((8 + 2√15) )/√4 = 1/2 × √((8 + 2√15) )/2 = √((8 + 2√15) )/4 ∴ sin 𝒙/𝟐 = √((𝟖 + 𝟐√𝟏𝟓) )/𝟒 We know that tan x = sin𝑥/𝑐𝑜𝑠𝑥 Replacing x with 𝑥/2 tan 𝒙/𝟐 = 𝒔𝒊𝒏〖 𝒙/𝟐〗/〖𝒄𝒐𝒔 〗〖𝒙/𝟐〗 = (√((8 + 2√15) )/4)/(√((8 −2√15))/4) = √((8 + 2√15) )/√((8 − 2√15) ) = √(((8 + 2√15))/((8 − 2√15) )×((8 + 2√15))/((8 + 2√15) )) = √((8 + 2√15)2/(8 − 2√15)(8 + 2√15) ) = √(((8 + 2√15))/((8 − 2√15) )×((8 + 2√15))/((8 + 2√15) )) = √((8 + 2√15)2/(8 − 2√15)(8 + 2√15) ) = √((8 + 2√15)2/((82 −(2√15)2) )) = √((8 + 2√15)2/((64 − (4 × 15)) )) = √((8 + 2√15)2/((64 − 60) )) = √((8 + 2√15)2/4) = √((8 + 2√15)2/22) = √((((8 + 2√15))/2)^2 ) = √((((8 + 2√15))/2)^2 ) = ((𝟖 + 𝟐√𝟏𝟓))/𝟐 = 2(4 + √15)/2 \ Hence, tan 𝒙/𝟐 = (𝟒 + √𝟏𝟓)