Misc 8 - Chapter 3 Class 11 Trigonometric Functions

Transcript

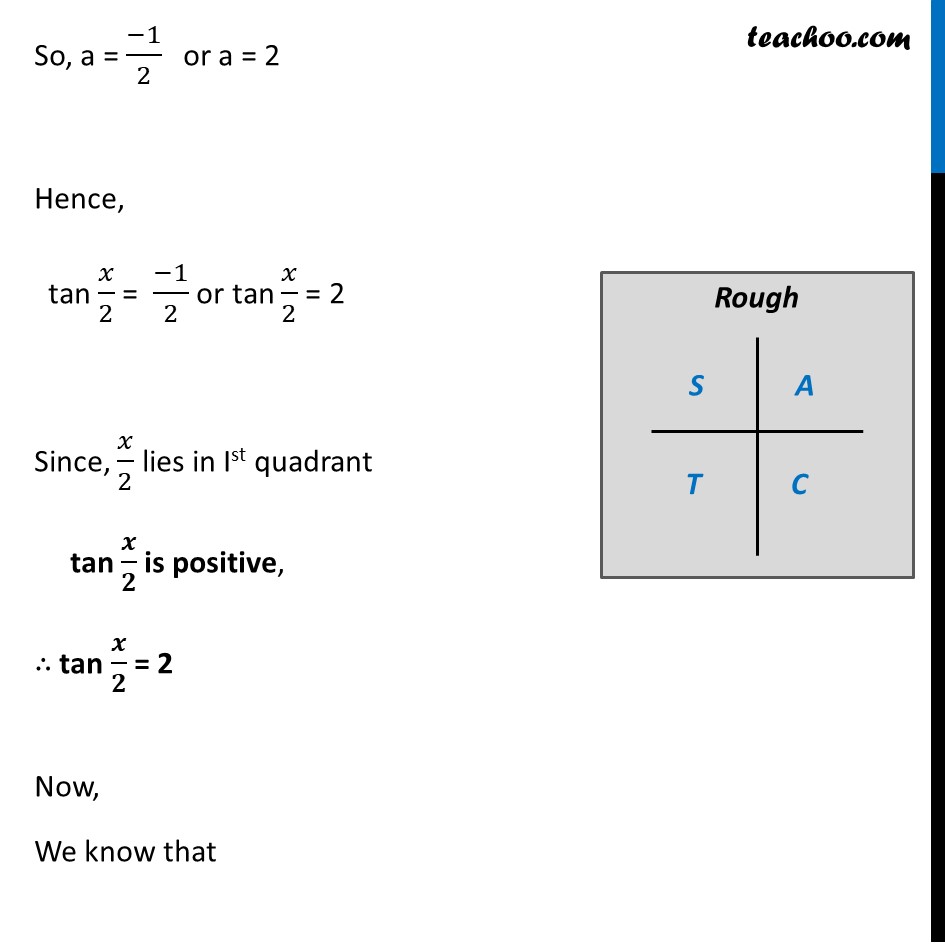
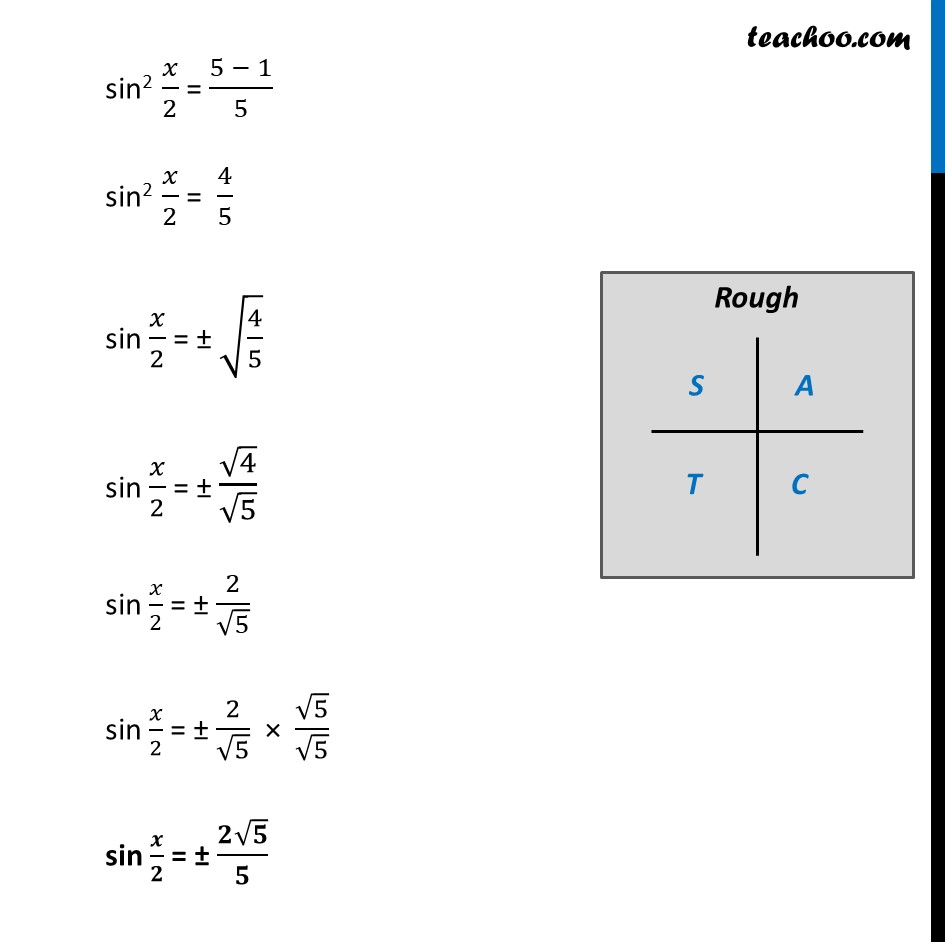
Misc 8 Find the value of sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 in each of the following : tan⁡𝑥 = – 4/3 , 𝑥 in quadrant II Given that x is in quadrant II So, 90° < x < 180° Dividing by 2 all sides (90°)/2 < 𝑥/2 < (180°)/2 45° < 𝑥/2 < 90° So, 𝑥/2 lies in Ist quadrant In 1st quadrant, sin , cos & tan are positive ∴ sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 are positive Given tan x = (−4)/3 We know that tan 2x = (2 𝑡𝑎𝑛⁡𝑥)/(1 − 𝑡𝑎𝑛2𝑥) Replacing x with 𝑥/2 tan (2𝑥/2) = (2 𝑡𝑎𝑛⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) tan x = (2 𝑡𝑎𝑛⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) (2 tan⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) = −4/3 −4/3 = (2 tan⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) –4(2𝑥/2) = 3× 2 tan (𝑥/2) –4 × 1 – (–4) × tan2 (𝑥/2) = 6 tan (𝑥/2) –4 × 1 – (–4) × tan2 (𝑥/2) = 6 tan (𝑥/2) –4 + 4 tan2 (𝑥/2) = 6 tan (𝑥/2) –4 + 4 tan2 (𝑥/2) – 6 tan (𝑥/2) = 0 Replacing tan 𝒙/𝟐 by a Our equation becomes –4 + 4a2 – 6a = 0 4a2 – 6a – 4 = 0 4a2 – 8a + 2a – 4 = 0 4a(a – 2) + 2 (a – 2) = 0 (4a + 2) (a – 2) = 0 Hence 4a + 2 = 0 4a = −2 a = (−2)/( 4) a = (−1)/2 So, a = (−1)/2 or a = 2 Hence, tan 𝑥/2 = (−1)/2 or tan 𝑥/2 = 2 Since, 𝑥/2 lies in Ist quadrant tan 𝑥/2 is positive, ∴ tan 𝒙/𝟐 = 2 Now, We know that 1 + tan2 x = sec2 x Replacing x with 𝑥/2 1 + tan2 𝑥/2 = sec2 𝑥/2 1 + (2)2 = sec2 𝑥/2 1 + 4 = sec2 x/2 1 + 4 = sec2 x/2 5 = sec2 𝑥/2 sec2 𝑥/2 = 5 sec 𝑥/2 = ± √5 Since 𝑥/2 lie on the 1st Quadrant, sec 𝑥/2 is positive in the 1st Quadrant So, sec 𝒙/𝟐 = √𝟓 Therefore, cos 𝒙/𝟐 = 𝟏/√𝟓 Now, We know that sin2x + cos2x = 1 Replacing x with 𝑥/2 sin2 𝑥/2 + cos2 𝑥/2 = 1 sin2 𝑥/2 = 1 – cos2 𝑥/2 Putting cos 𝑥/2 = √5/5 sin2 𝑥/2 = 1 – (√5/5)2 sin2 𝑥/2 = 1 – 5/25 sin2 𝑥/2 = 1 – 1/5 sin2 𝑥/2 = (5 − 1)/5 sin2 𝑥/2 = 4/5 sin 𝑥/2 = ± √(4/5) sin 𝑥/2 = ± √4/√5 sin 𝑥/2 = ± 2/√5 sin 𝑥/2 = ± 2/√5 × √5/√5 sin 𝑥/2 = ± (2√5)/5 Since 𝑥/2 lies on the 1st Quadrant sin 𝑥/2 is positive in the 1st Quadrant So, sin 𝒙/𝟐 = (𝟐√𝟓)/𝟓 Therefore, tan 𝑥/2 = 2 , cos 𝒙/𝟐 = √𝟓/𝟓 & sin 𝒙/𝟐 = (𝟐√𝟓)/𝟓