The set of all points where the function f(x)=x+|x| is differentiable, is
(a) (0,∞) (b) (-∞,0)
(c) (-∞,0)∪(0,∞) (d) (-∞,∞)
This question is similar to Question-15 NCERT-Exemplar-MCQs


CBSE Class 12 Sample Paper for 2024 Boards
CBSE Class 12 Sample Paper for 2024 Boards
Last updated at Feb. 10, 2025 by Teachoo
This question is similar to Question-15 NCERT-Exemplar-MCQs



Transcript
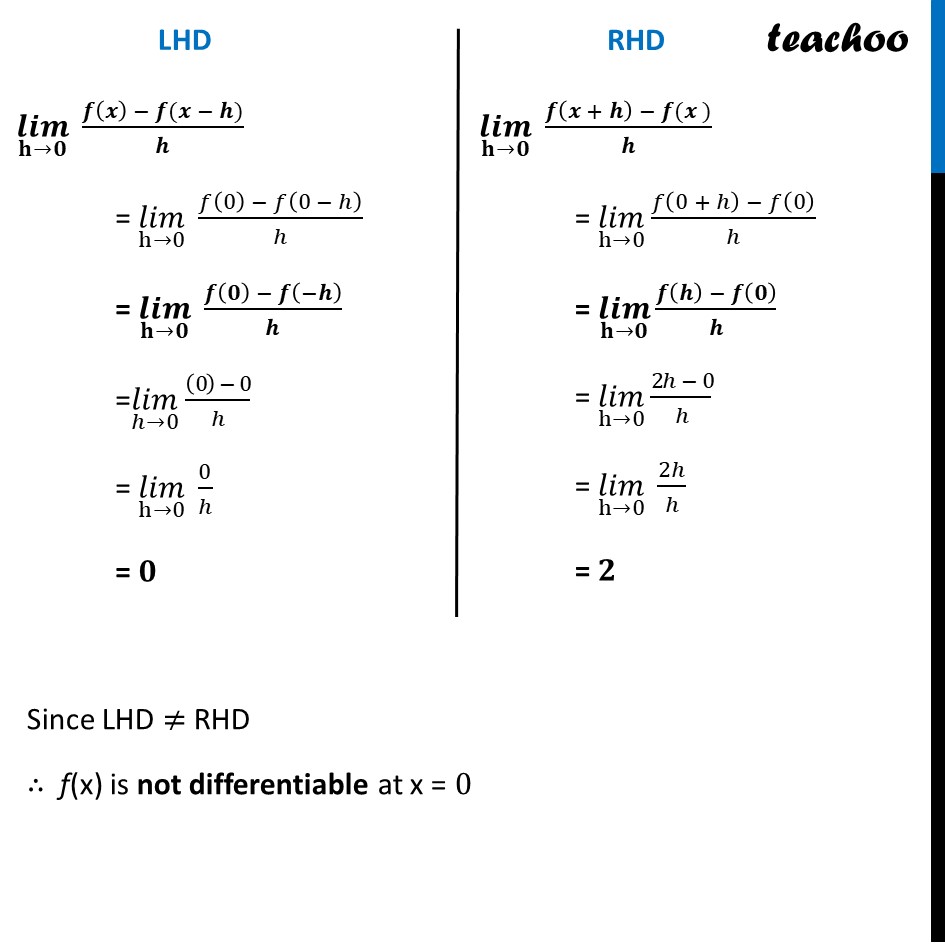
𝑓(𝑥) = 𝑥+|𝑥| = {█(𝑥+𝑥, 𝑥≥0@𝑥−𝑥, 𝑥 <0)┤ = {█(2𝑥, 𝑥≥0@0, 𝑥<0)┤ Now, f(x) is a differentiable at x = 0 if LHD = RHD (𝒍𝒊𝒎)┬(𝐡→𝟎) (𝒇(𝒙) − 𝒇(𝒙 − 𝒉))/𝒉 = (𝑙𝑖𝑚)┬(h→0) (𝑓(0) − 𝑓(0 − ℎ))/ℎ = (𝒍𝒊𝒎)┬(𝐡→𝟎) (𝒇(𝟎) − 𝒇(−𝒉))/𝒉 =(𝑙𝑖𝑚)┬(ℎ→0) (2(0) − 0)/ℎ = (𝑙𝑖𝑚)┬(h→0) 0/ℎ = 𝟎 (𝒍𝒊𝒎)┬(𝐡→𝟎) (𝒇(𝒙 + 𝒉) − 𝒇(𝒙 ))/𝒉 = (𝑙𝑖𝑚)┬(h→0) (𝑓(0 + ℎ) − 𝑓(0))/ℎ = (𝒍𝒊𝒎)┬(𝐡→𝟎) (𝒇(𝒉) − 𝒇(𝟎))/𝒉 = (𝑙𝑖𝑚)┬(h→0) (2ℎ − 0)/ℎ = (𝑙𝑖𝑚)┬(h→0) 2ℎ/ℎ = 𝟐 Hence, we can say that f(x) is differentiable on R − {𝟎} or (−∞,𝟎)∪(𝟎,∞) So, the correct answer is (c)