Maths Crash Course - Live lectures + all videos + Real time Doubt solving!
Example 6 - Chapter 3 Class 11 Trigonometric Functions (Term 2)
Last updated at Feb. 12, 2020 by Teachoo
Examples
Example 1
Example 2 Important
Example 3
Example 4
Example 5 Important
Example 6 Important You are here
Example 7 Important
Example 8
Example 9 Important
Example 10
Example 11 Important
Example 12
Example 13
Example 14
Example 15
Example 16 Important
Example 17 Important
Example 18
Example 19
Example 20 Deleted for CBSE Board 2023 Exams
Example 21 Deleted for CBSE Board 2023 Exams
Example 22 Important Deleted for CBSE Board 2023 Exams
Example 23 Deleted for CBSE Board 2023 Exams
Example 24 Important Deleted for CBSE Board 2023 Exams
Example 25 Important
Example 26
Example 27 Important
Example 28 Important
Example 29 Important
Chapter 3 Class 11 Trigonometric Functions
Serial order wise
- Ex 3.1
- Ex 3.2
- Ex 3.3
- Ex 3.4
-
Examples
- Miscellaneous
Transcript
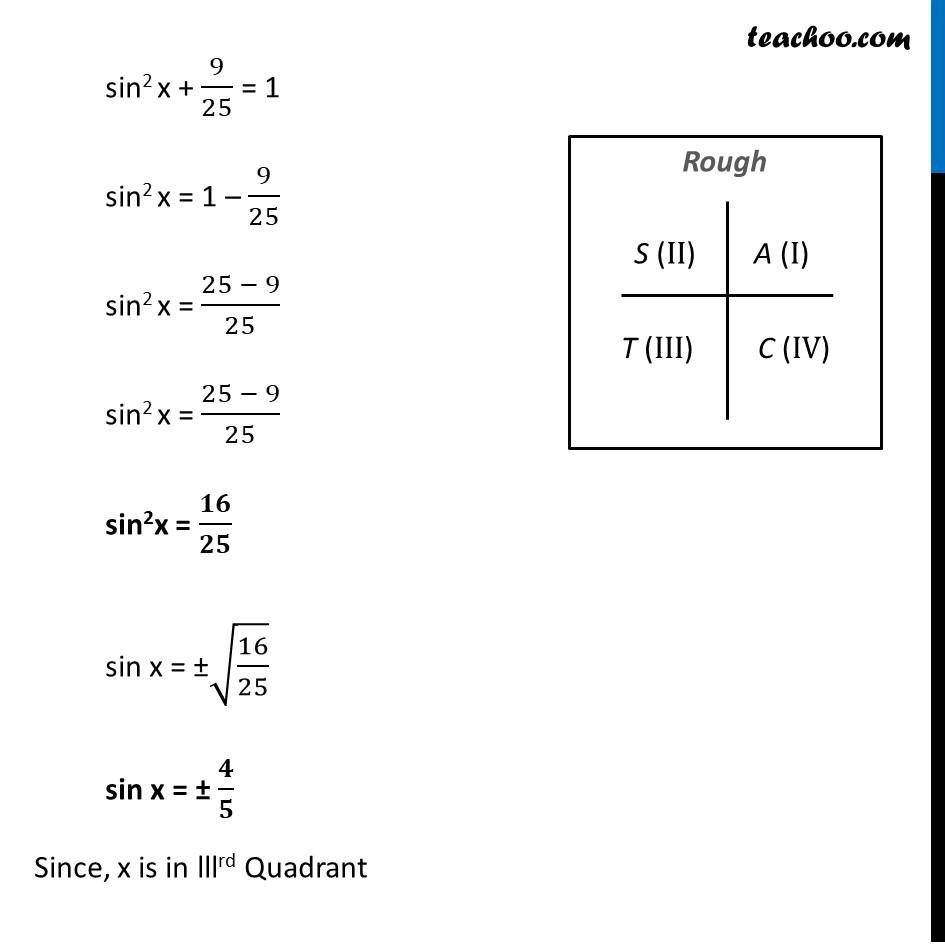
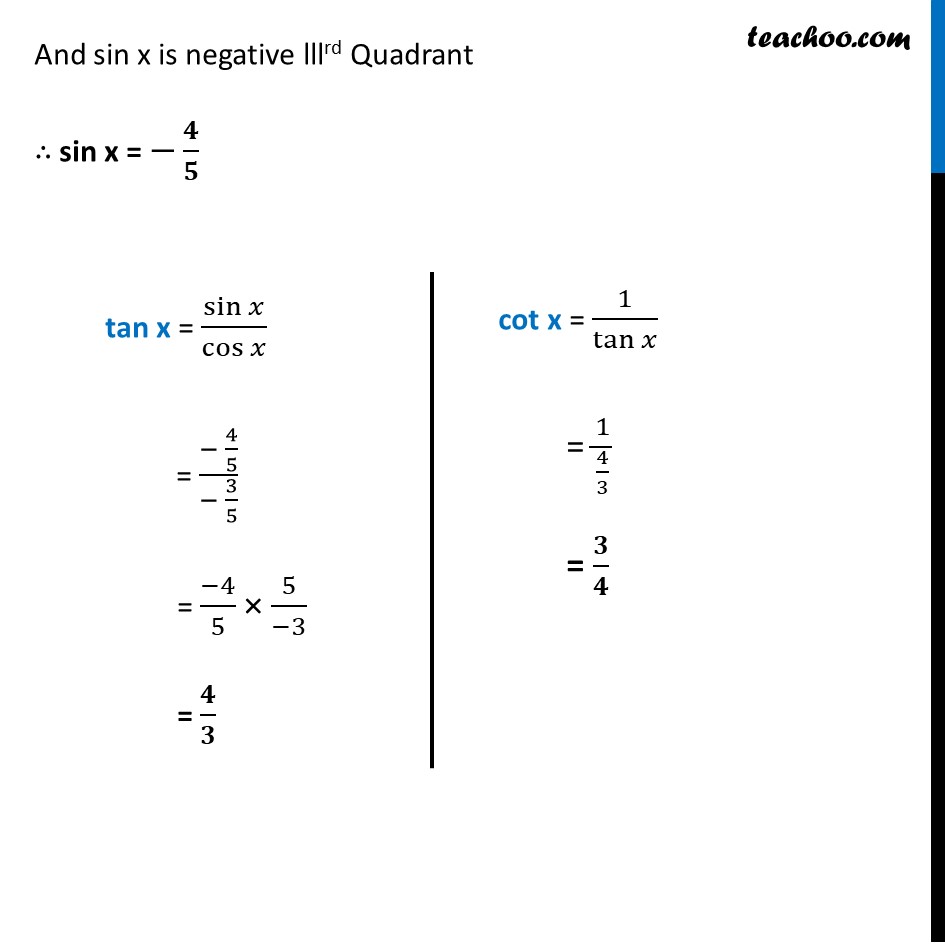
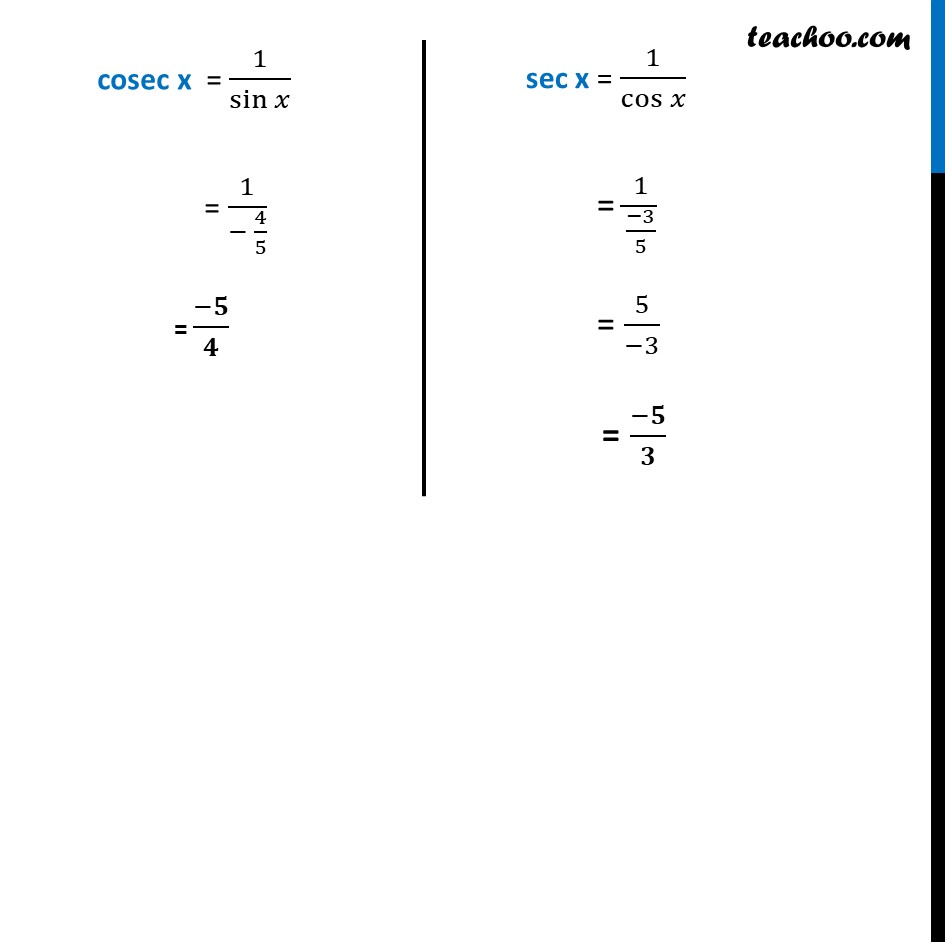
Example 6 If cos𝑥 = – 3/5 , x lies in third quadrant, find the values of other five trigonometric functions. Since x is in lllrd Quadrant sin and cos will be negative But tan will be positive Given cos x = (−3)/5 We know that sin2 x + cos2 x = 1 sin2 x + ((−3)/5)^2 = 1 sin2 x + 9/25 = 1 sin2 x = 1 – 9/25 sin2 x = (25 − 9)/25 sin2 x = (25 − 9)/25 sin2x = 16/25 sin x = ±√(16/25) sin x = ± 4/5 Since, x is in lllrd Quadrant And sin x is negative lllrd Quadrant ∴ sin x = −𝟒/𝟓 tan x = sin𝑥/cos𝑥 = (− 4/5)/(− 3/5) = (−4)/5 × 5/(−3) = 𝟒/𝟑 cot x = 1/tan𝑥 = 1/(4/3) = 𝟑/𝟒 cosec x = 1/sin𝑥 = 1/(− 4/5) = (−𝟓)/𝟒 sec x = 1/cos𝑥 = 1/((−3)/5) = 5/(−3) = (−𝟓)/𝟑
