CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard

CBSE Class 10 Sample Paper for 2023 Boards - Maths Standard →
Class 10
Solutions of Sample Papers for Class 10 Boards

Question 22 - CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Last updated at April 16, 2024 by

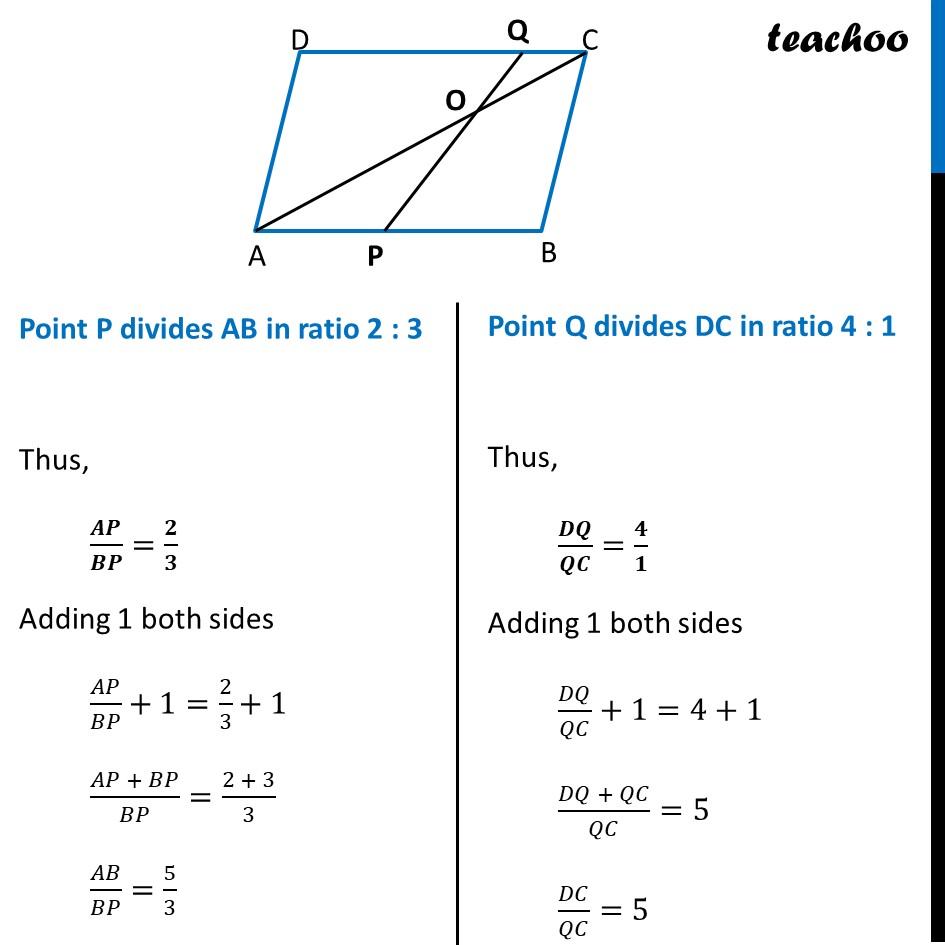
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA

Slide50.JPG

Slide53.JPG
Slide54.JPG
Slide55.JPG
Slide56.JPG

Transcript

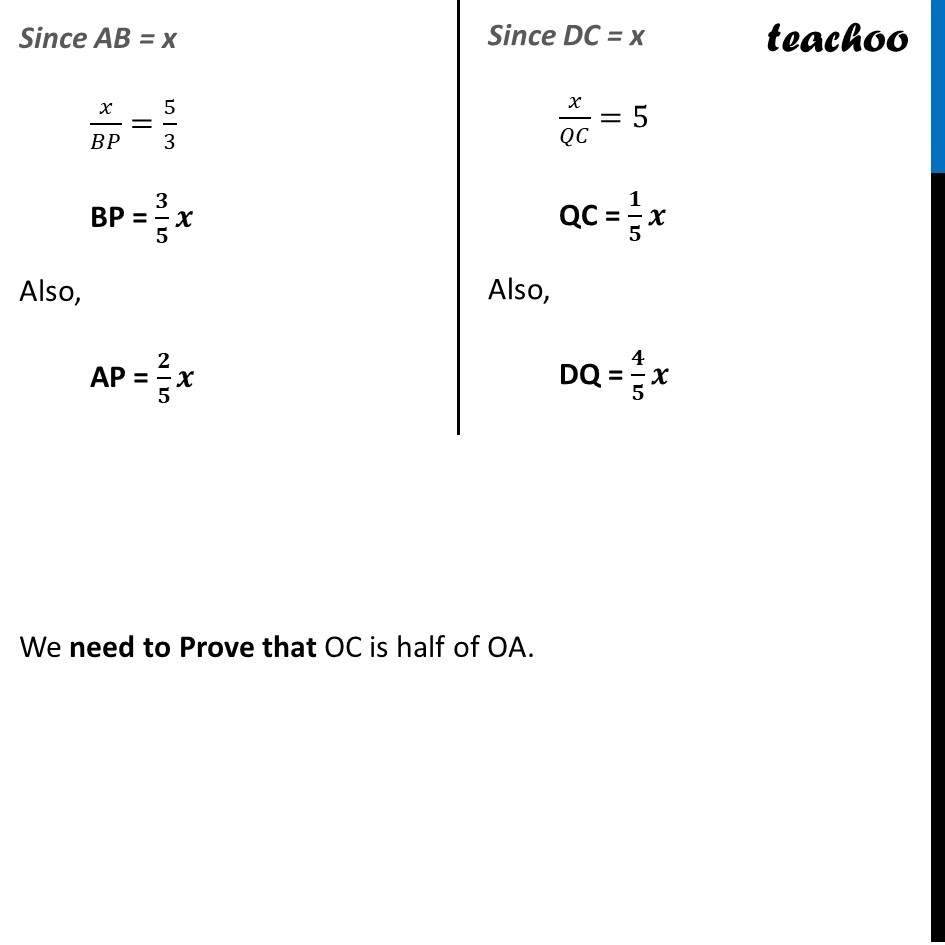
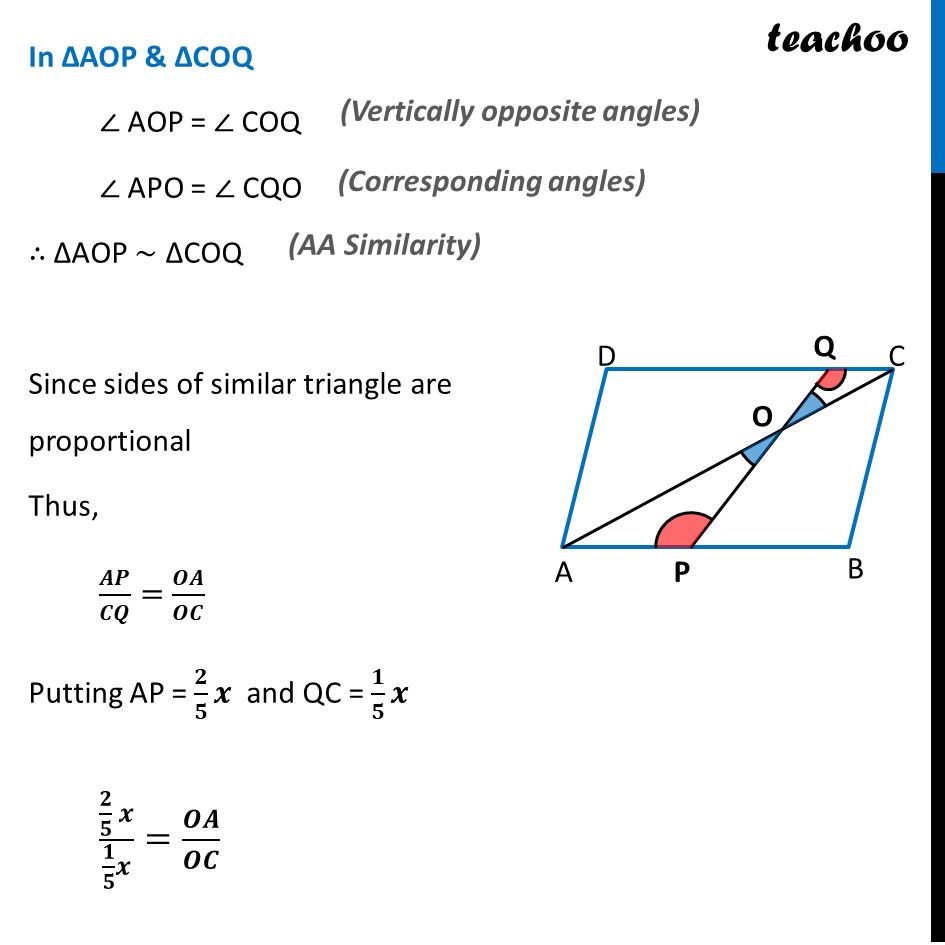
Since opposite sides of parallelogram are equal AB = CD Let AB = CD = x Point P divides AB in ratio 2 : 3 Thus, 𝑨𝑷/𝑩𝑷=𝟐/𝟑 Adding 1 both sides 𝐴𝑃/𝐵𝑃+1=2/3+1 (𝐴𝑃 + 𝐵𝑃)/𝐵𝑃=(2 + 3)/3 𝐴𝐵/𝐵𝑃=5/3 Since AB = x 𝑥/𝐵𝑃=5/3 BP = 𝟑/𝟓 𝒙 Also, AP = 𝟐/𝟓 𝒙 Point P divides AB in ratio 2 : 3 Thus, 𝑨𝑷/𝑩𝑷=𝟐/𝟑 Adding 1 both sides 𝐴𝑃/𝐵𝑃+1=2/3+1 (𝐴𝑃 + 𝐵𝑃)/𝐵𝑃=(2 + 3)/3 𝐴𝐵/𝐵𝑃=5/3Point Q divides DC in ratio 4 : 1 Thus, 𝑫𝑸/𝑸𝑪=𝟒/𝟏 Adding 1 both sides 𝐷𝑄/𝑄𝐶+1=4+1 (𝐷𝑄 + 𝑄𝐶)/𝑄𝐶=5 𝐷𝐶/𝑄𝐶=5 In ΔAOP & ΔCOQ ∠ AOP = ∠ COQ ∠ APO = ∠ CQO ∴ ΔAOP ~ ΔCOQ Since sides of similar triangle are proportional Thus, 𝑨𝑷/𝑪𝑸=𝑶𝑨/𝑶𝑪 Putting AP = 𝟐/𝟓 𝒙 and QC = 𝟏/𝟓 𝒙 (𝟐/𝟓 𝒙)/(𝟏/𝟓 𝒙)=𝑶𝑨/𝑶𝑪 2/1=𝑂𝐴/𝑂𝐶 𝐎𝐂=𝟏/𝟐 𝐎𝐀 ∴ OC is half of OA Hence proved

Go Ad-free
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.