Ex 3.3, 3 - Chapter 3 Class 11 Trigonometric Functions
Last updated at August 8, 2026 by Teachoo
Finding Value of trignometric functions, given angle
Negative Angle Identities
You are here
You are here
Chapter 3 Class 11 Trigonometric Functions
Concept wise
- Radian measure - Conversion
- Arc length
- Finding Value of trignometric functions, given other functions
-
Finding Value of trignometric functions, given angle
- (x + y) formula
- 2x 3x formula - Proving
- 2x 3x formula - Finding value
- cos x + cos y formula
- 2 sin x sin y formula
- Finding Principal solutions
- Finding General Solutions
- Sine and Cosine Formula
Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 10 questions, selected from your answers, mistakes, and progress.
Transcript
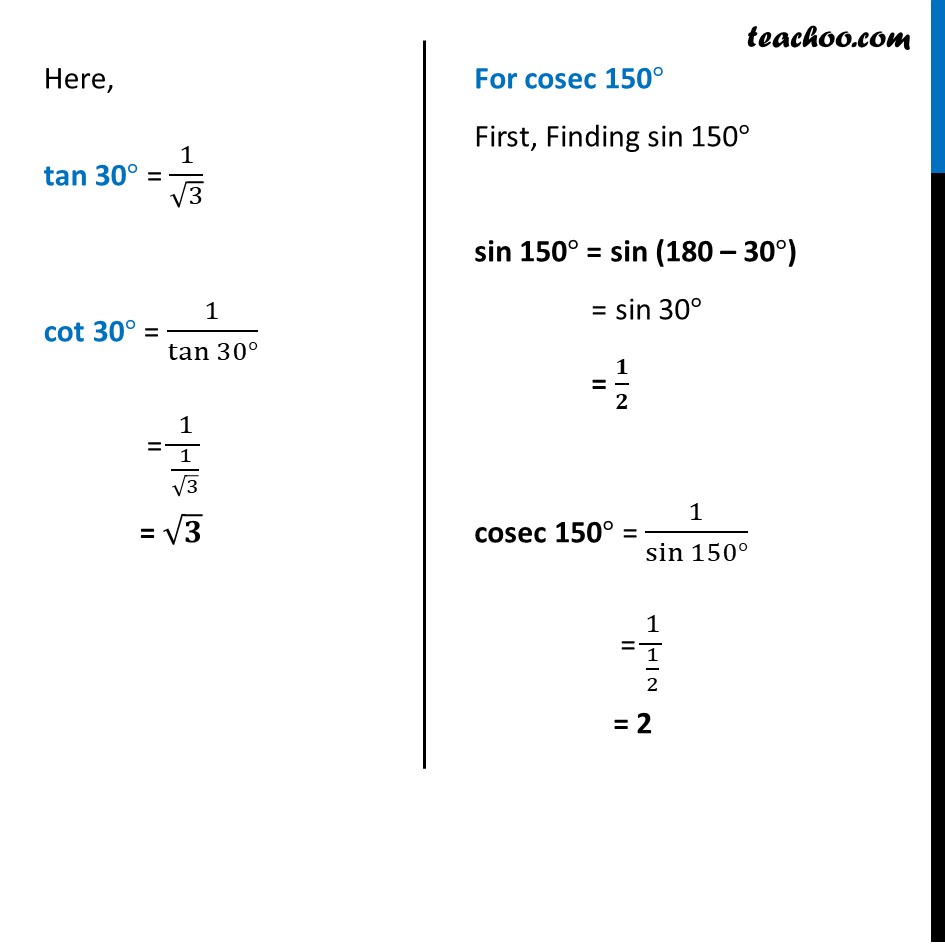
Ex 3.3, 3 Prove that cot2 π/6 + cosec 5π/6 + 3 tan2 π/6 = 6 Solving L.H.S. cot2 π/6 + cosec 5π/6 + 3 tan2 π/6 Putting π = 180° = cot2(180/6) + cosec((5 ×180)/6) + 3 tan2(180/6) = cot2 30° + cosec (150°) + 3tan2 30° Here, tan 30° = 1/√3 cot 30° = 1/tan〖30°〗 = 1/(1/√3) = √𝟑 For cosec 150° First, Finding sin 150° sin 150° = sin (180 – 30°) = sin 30° = 𝟏/𝟐 cosec 150° = 1/sin〖150°〗 = 1/(1/2) = 2 Putting values cot2 30° + cosec (150°) + 3tan2 30° = (√𝟑)2 + 2 + 3 × (𝟏/√𝟑)^𝟐 = 3 + 2 + 3 × 1/3 = 3 + 2 + 1 = 6 = R.H.S Hence proved
