CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard
You are here
CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard
Last updated at Dec. 13, 2024 by Teachoo
This question is similar to Example 9 Chapter 7 Class 10 Coordinate Geometary
Transcript
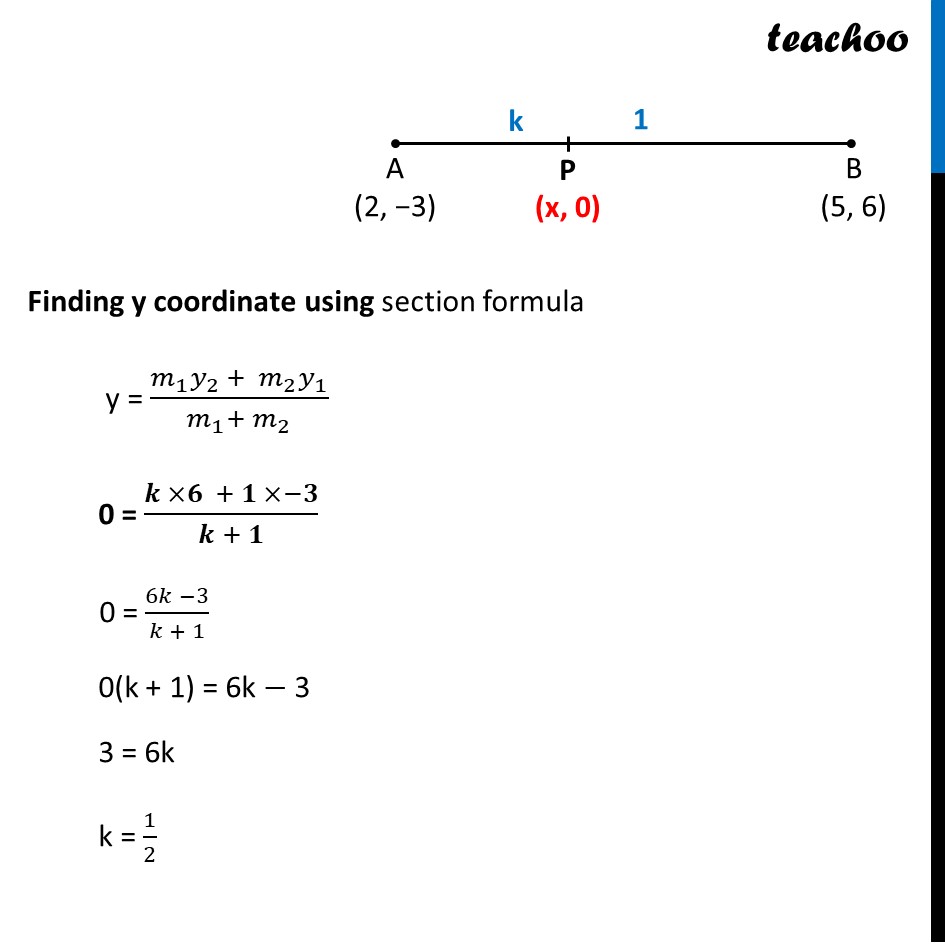
Question 6 What is the ratio in which the line segment joining (2,-3) and (5, 6) is divided by x-axis? (a) 1:2 (b) 2:1 (c) 2:5 (d) 5:2 Let the points be A(2, −3) & B(5, 6) Let P be the point which divides line segment AB in the ratio k : 1 Since Point P is on x−axis, ∴ Its y coordinate is 0. So, it is of the form P(x, 0) Finding y coordinate using section formula y = (𝑚_1 𝑦_2 + 𝑚_2 𝑦_1)/(𝑚_1+ 𝑚_2 ) 0 = (𝒌 ×𝟔 + 𝟏 ×−𝟑)/(𝒌 + 𝟏) 0 = (6𝑘 −3)/(𝑘 + 1) 0(k + 1) = 6k − 3 3 = 6k k = 1/2 Hence the required ratio will be 1/2 : 1 i.e 1 : 2 So, the correct answer is (a)
