Ex 3.1, 5 - Chapter 3 Class 11 Trigonometric Functions

Transcript

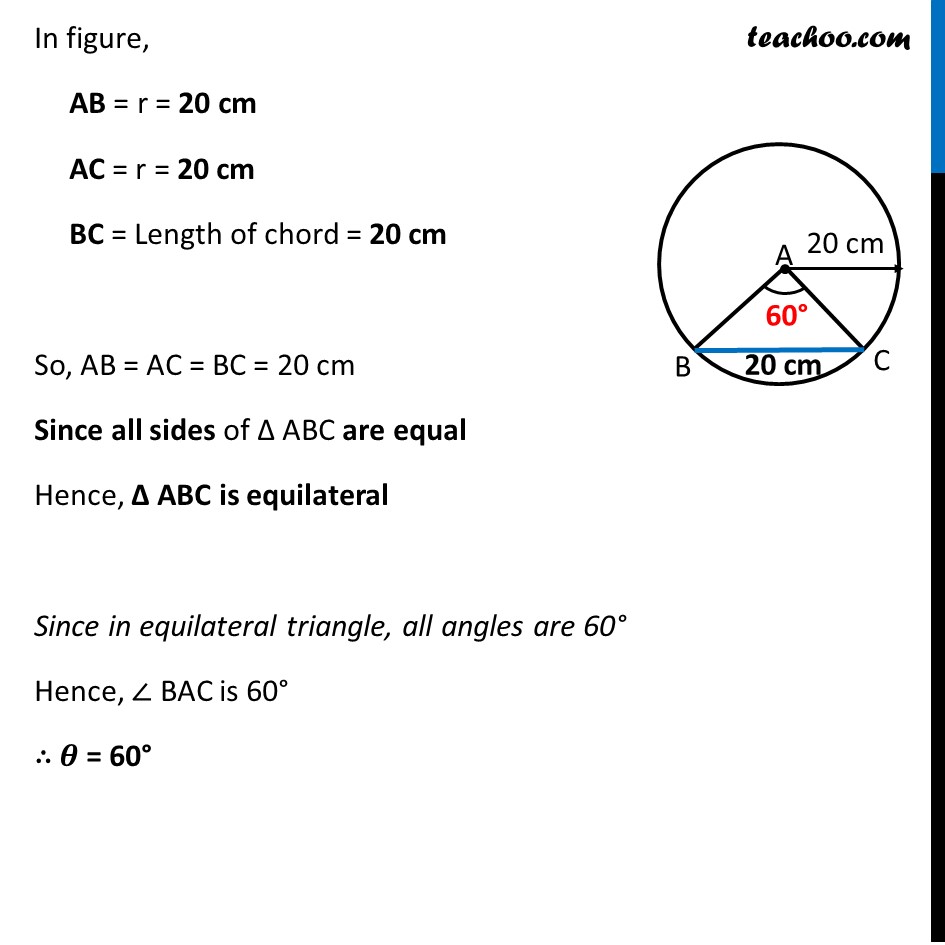
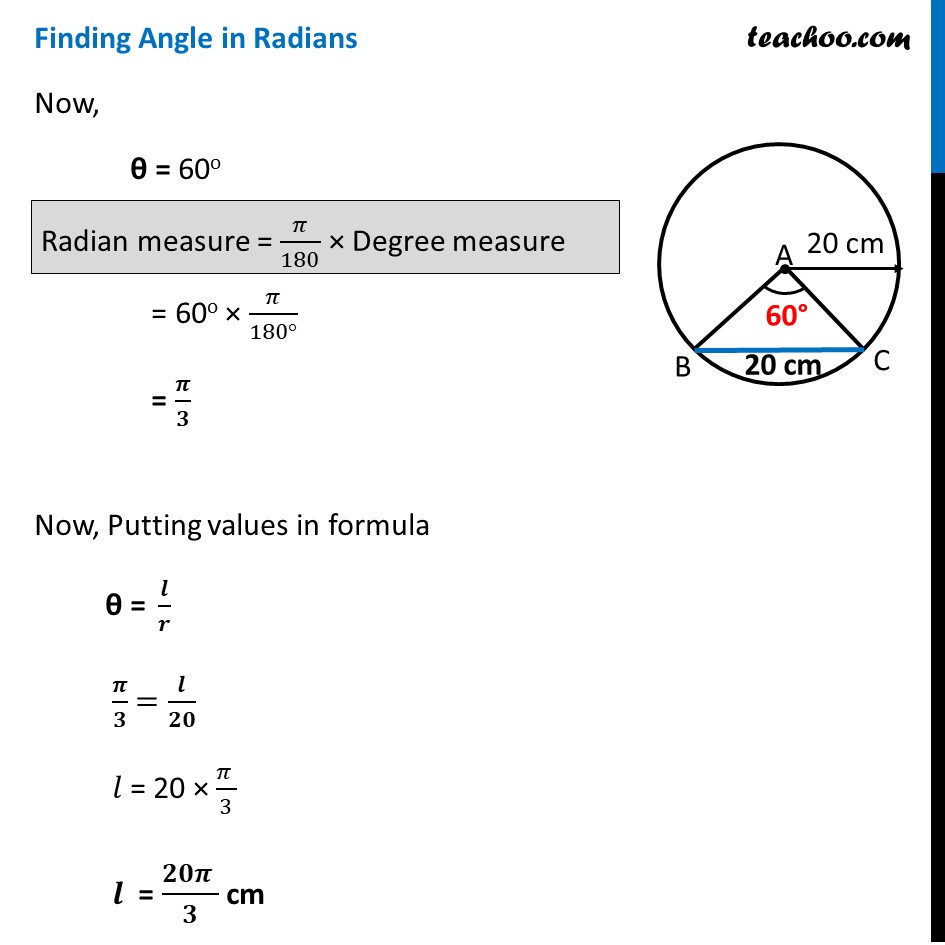
Ex 3.1, 5 In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord. Given Diameter = 40 cm Radius = r = 20 cm We need to find length of minor arc of the chord. Thus, we use formula θ = 𝒍/𝒓 to find length of arc In figure, AB = r = 20 cm AC = r = 20 cm BC = Length of chord = 20 cm So, AB = AC = BC = 20 cm Since all sides of Δ ABC are equal Hence, Δ ABC is equilateral Since in equilateral triangle, all angles are 60° Hence, ∠ BAC is 60° ∴ 𝜽 = 60° Finding Angle in Radians Now, θ = 60o = 60o × 𝜋/(180°) = 𝝅/𝟑 Now, Putting values in formula "θ = " 𝒍/𝒓 𝝅/𝟑 =𝒍/𝟐𝟎 𝑙 = 20 × (𝜋 )/3 𝒍 = (𝟐𝟎𝝅 )/𝟑 cm