Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class
Example 8 - Chapter 2 Class 11 Relations and Functions
Last updated at May 29, 2023 by Teachoo
Examples
Example 1
Example 2
Example 3 Important
Example 4 Important
Example 5
Example 6 Important
Example 7
Example 8 Important You are here
Example 9 Important
Example 10
Example 11 (i)
Example 11 (ii) Important
Example 11 (iii) Important
Example 12
Example 13
Example 14 Important
Example 15 Important
Example 16
Example 17 Important
Example 18
Example 19
Example 20 Important
Example 21 Important
Example 22 Important
Chapter 2 Class 11 Relations and Functions
Serial order wise
- Ex 2.1
- Ex 2.2
- Ex 2.3
-
Examples
- Miscellaneous
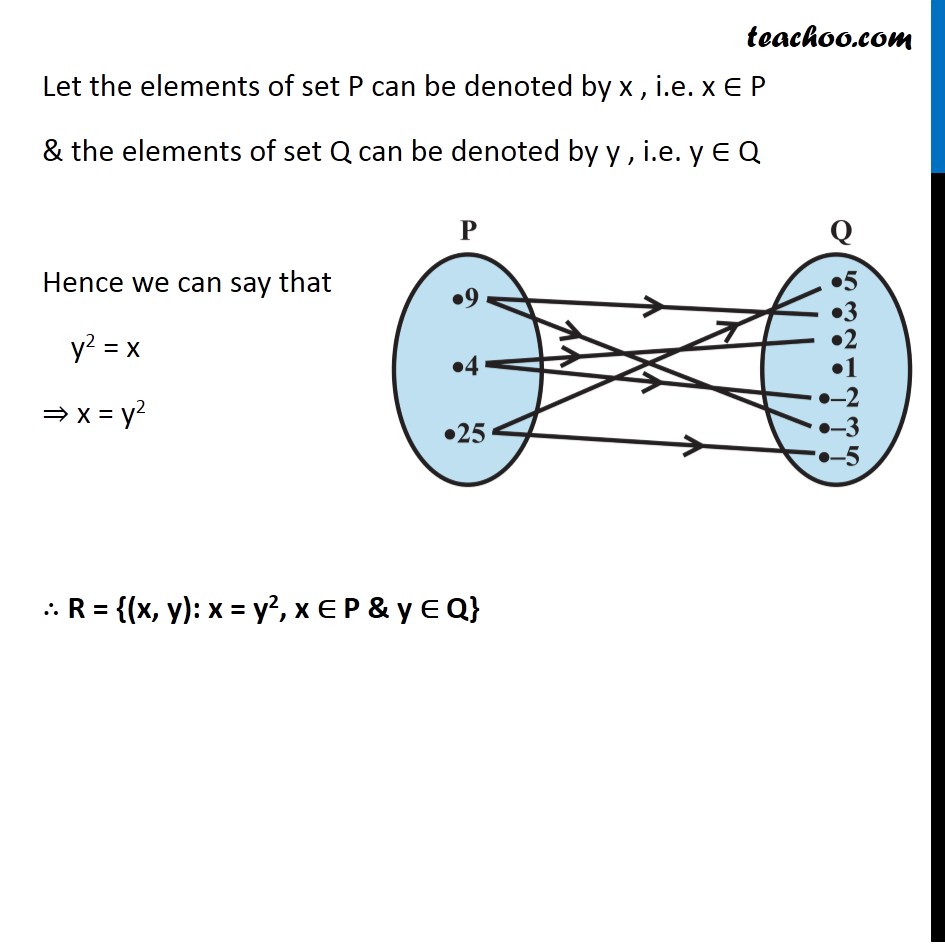
Transcript
Example 8 The figure shows a relation between the sets P and Q. Write this relation in set-builder form Note that (3)2 = 9 (–3)2 = 9 (2)2 = 4 (–2)2 = 4 (5)2 = 25 (–5)2 = 25 Let the elements of set P can be denoted by x , i.e. x ∈ P & the elements of set Q can be denoted by y , i.e. y ∈ Q Hence we can say that y2 = x ⇒ x = y2 ∴ R = {(x, y): x = y2, x ∈ P & y ∈ Q} Example 8 The figure shows a relation between the sets P and Q. Write this relation (ii) in roster form. What is its domain and range? In roster form Relation R = {(9, 3), (9, −3), (4, 2), (4, −2), (25, 5) (25, −5)} Domain = Set of first elements of Relation = {9, 4, 25} Range = Set of second elements of Relation = {3, −3, 2, −2, 5, −5}
