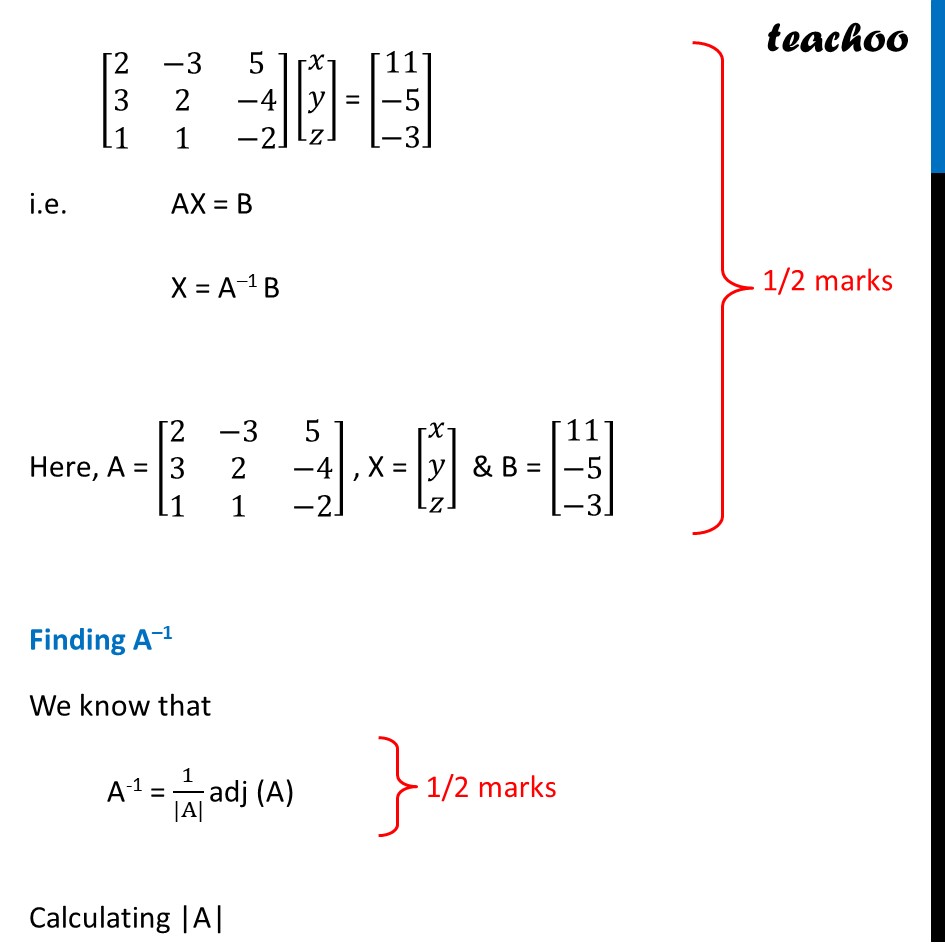
If A=[2&-3&5 3&2&-4 1&1&-2)], find A -1 . Use A -1 )to solve the following system of equations 2𝑥 − 3𝑦 + 5𝑧 = 11, 3x + 2y−4z, 𝑥 + 𝑦 − 2𝑧 = −3
![[Sample Paper] If A = [], find A^-1. Use A-1 to solve the system of - CBSE Class 12 Sample Paper for 2023 Boards](https://cdn.teachoo.com/b2641319-662c-494e-a3c6-365b66005423/slide25.jpg)



CBSE Class 12 Sample Paper for 2023 Boards
CBSE Class 12 Sample Paper for 2023 Boards
Last updated at December 13, 2024 by Teachoo
![[Sample Paper] If A = [], find A^-1. Use A-1 to solve the system of - CBSE Class 12 Sample Paper for 2023 Boards](https://cdn.teachoo.com/b2641319-662c-494e-a3c6-365b66005423/slide25.jpg)






Transcript
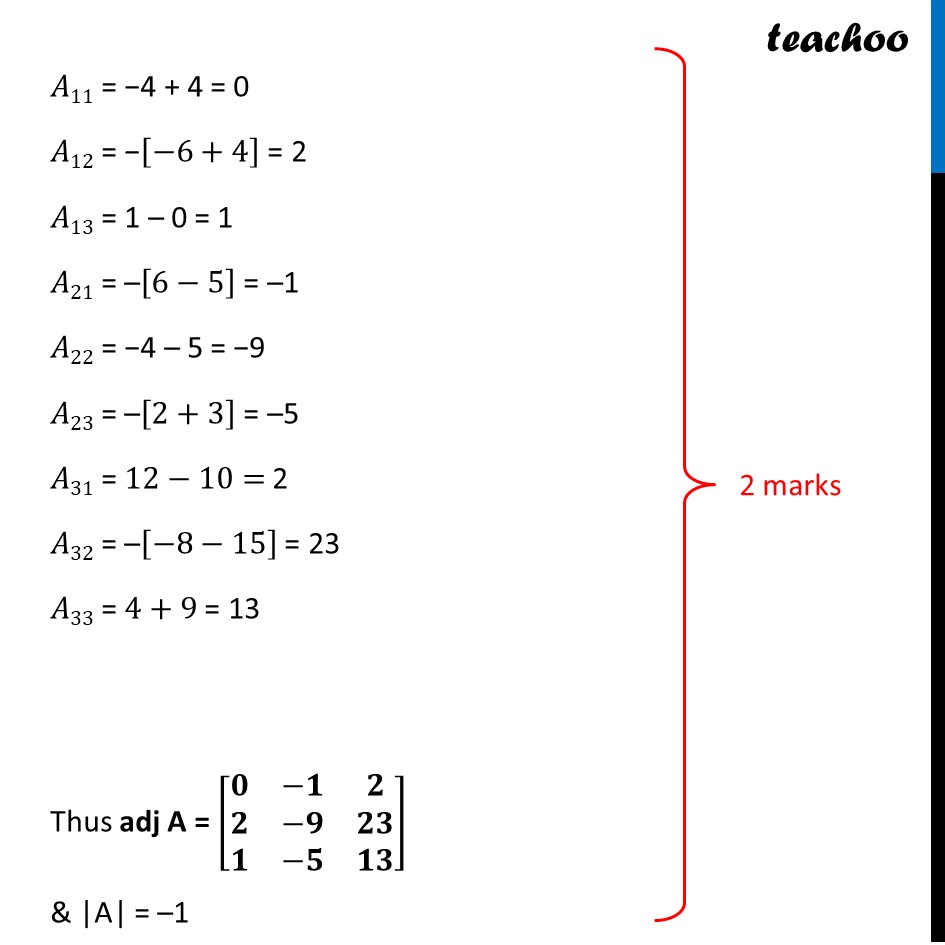
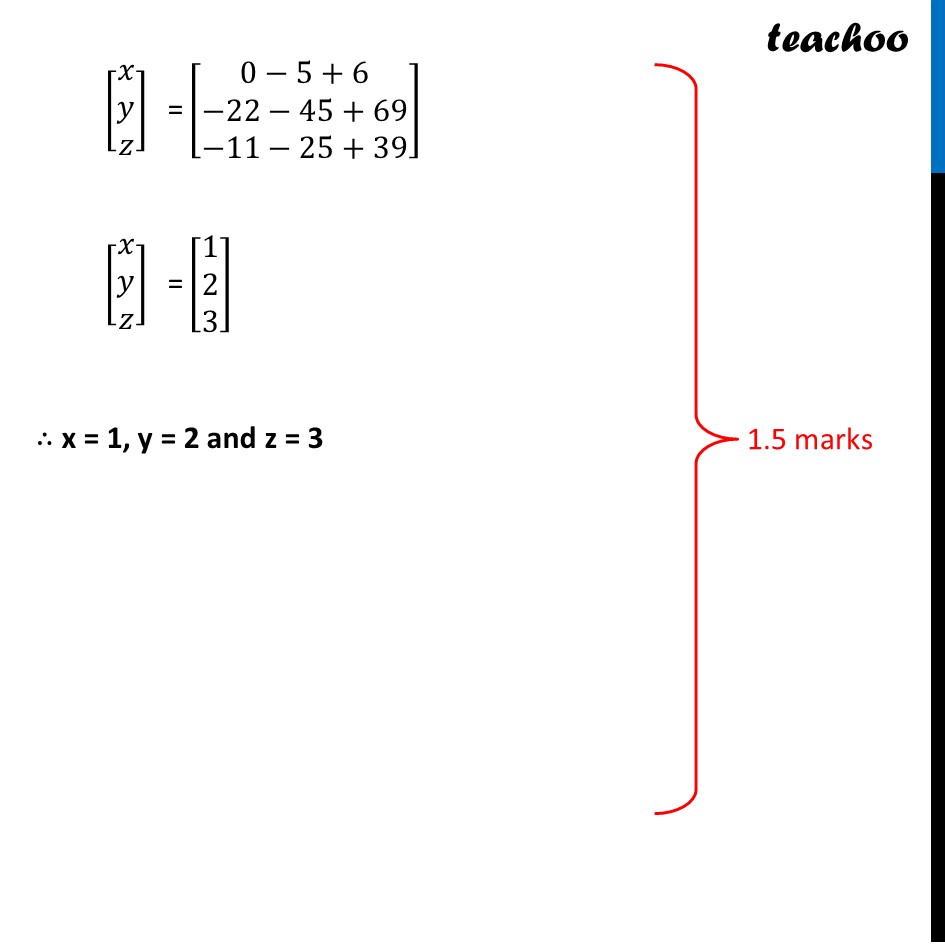
Question 35 If A=[■8(2&−3&5@3&2&−4@1&1&−2)], find 𝐴^(−1). Use 𝐴^(−1)to solve the following system of equations 2𝑥 − 3𝑦 + 5𝑧 = 11, 3x + 2y − 4z = −5, 𝑥 + 𝑦 − 2𝑧 = −3The equations can be written as 2𝑥 − 3𝑦 + 5𝑧 = 11 3x + 2y − 4z = −5 𝑥 + 𝑦 − 2𝑧 = −3 So, the equation is in the form of [■8(2&−3&5@3&2&−4@1&1&−2)][■8(𝑥@𝑦@𝑧)] = [■8(11@−5@−3)] i.e. AX = B X = A–1 B Here, A = [■8(2&−3&5@3&2&−4@1&1&−2)] , X = [■8(𝑥@𝑦@𝑧)] & B = [■8(11@−5@−3)] Finding A–1 We know that A-1 = 1/(|A|) adj (A) Calculating |A| |A|= |■8(2&−3&5@3&2&−4@1&1&−2)| = 2(−4 + 4) + 3 (−6 + 4) + 5 (3 – 2) = 2(0) + 3(−2) + 5(1) = −1 Since |A|≠ 0 ∴ The system of equation is consistent & has a unique solution Now finding adj (A) adj A = [■8(A11&A12&A13@A21&A22&A23@A31&A32&A33)]^′ = [■8(A11&A21&A31@A12&A22&A32@A13&A23&A33)] A = [■8(2&−3&5@3&2&−4@1&1&−2)] 𝐴11 = −4 + 4 = 0 𝐴12 = −[−6+4] = 2 𝐴13 = 1 – 0 = 1 𝐴21 = –[6−5] = –1 𝐴22 = −4 – 5 = −9 𝐴23 = –[2+3] = –5 𝐴31 = 12−10= 2 𝐴32 = –[−8−15] = 23 𝐴33 = 4+9 = 13 Thus adj A = [■8(𝟎&−𝟏&𝟐@𝟐&−𝟗&𝟐𝟑@𝟏&−𝟓&𝟏𝟑)] & |A| = –1 Now, A-1 = 1/(|A|) adj A A-1 = 1/(−1) [■8(0&−1&2@2&−9&23@1&−5&13)] = [■8(𝟎&𝟏&−𝟐@−𝟐&𝟗&−𝟐𝟑@−𝟏&𝟓&−𝟏𝟑)] Now, X = A–1B [■8(𝑥@𝑦@𝑧)] = [■8(0&1&−2@−2&9&−23@−1&5&−13)][■8(11@−5@−3)] [■8(𝑥@𝑦@𝑧)]" =" [█(0(11)+1(−5)−2(−3)@−2(11)+9(−5)−23(−3)@(−1)(11)+5(−5)−13(−3))] " " [■8(𝑥@𝑦@𝑧)]" =" [■8(0−5+6@−22−45+69@−11−25+39)] " " [■8(𝑥@𝑦@𝑧)]" =" [■8(1@2@3)] "∴ x = 1, y = 2 and z = 3"