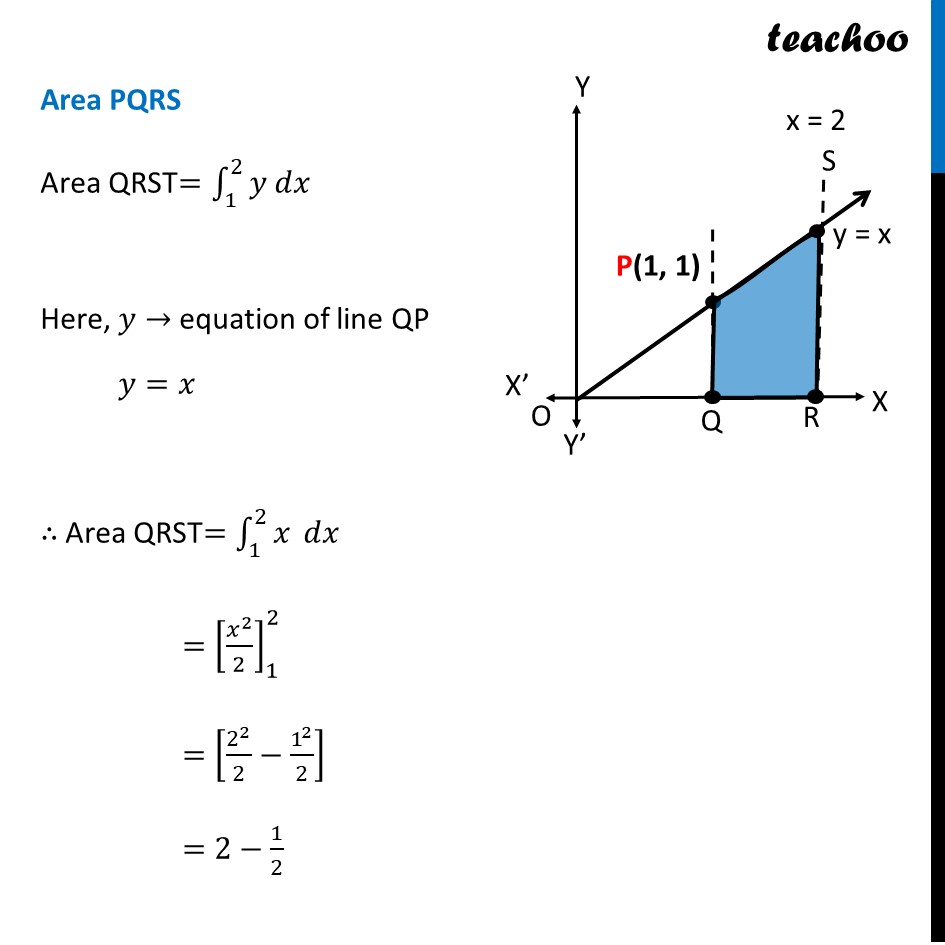
Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ x^2, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integration



CBSE Class 12 Sample Paper for 2023 Boards
CBSE Class 12 Sample Paper for 2023 Boards
Last updated at Dec. 13, 2024 by Teachoo









Transcript
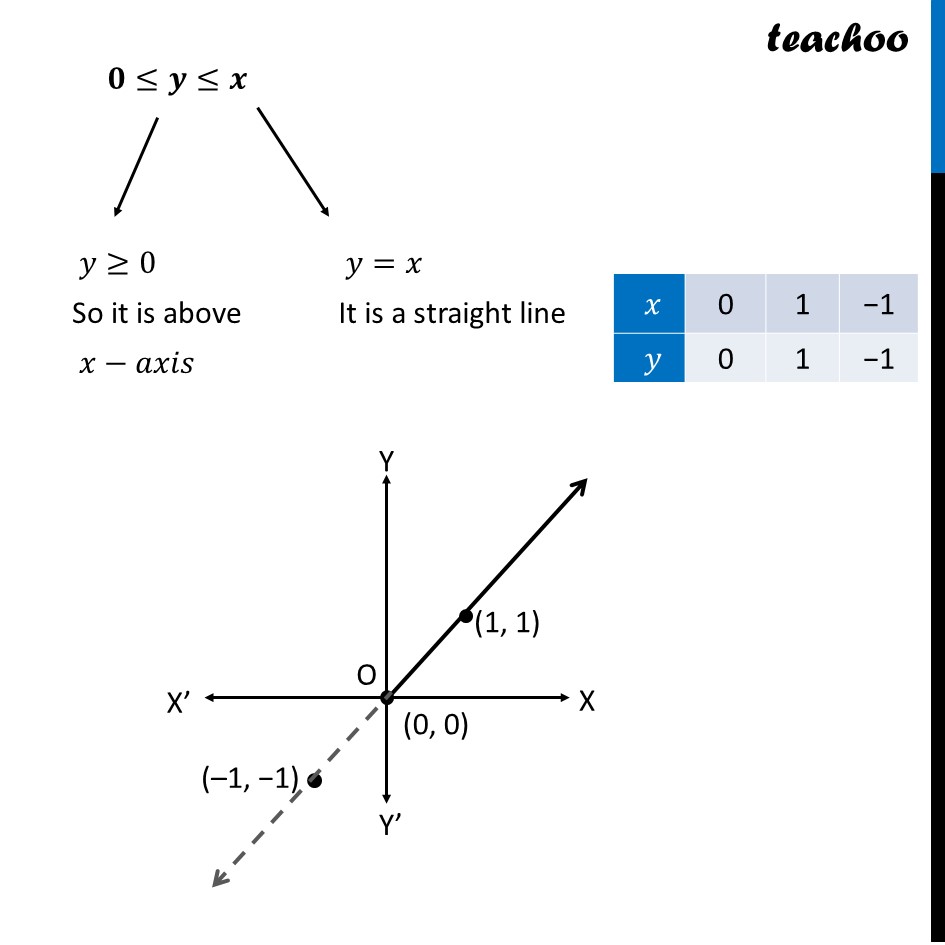
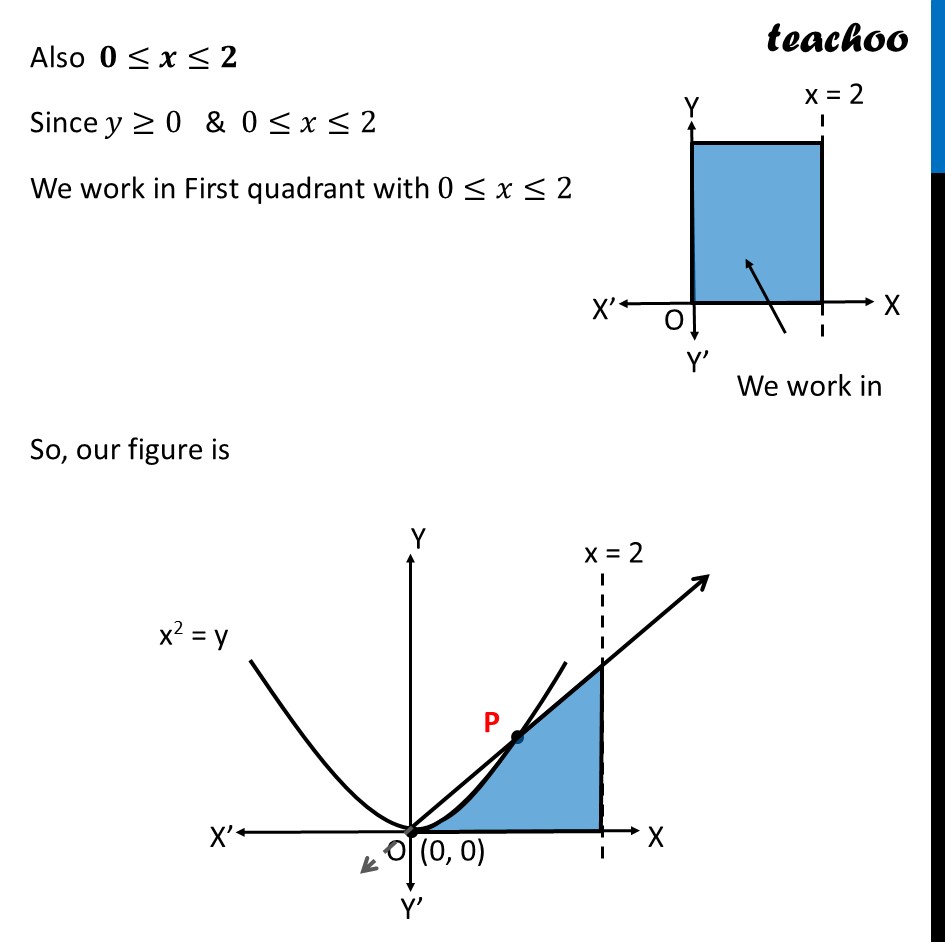
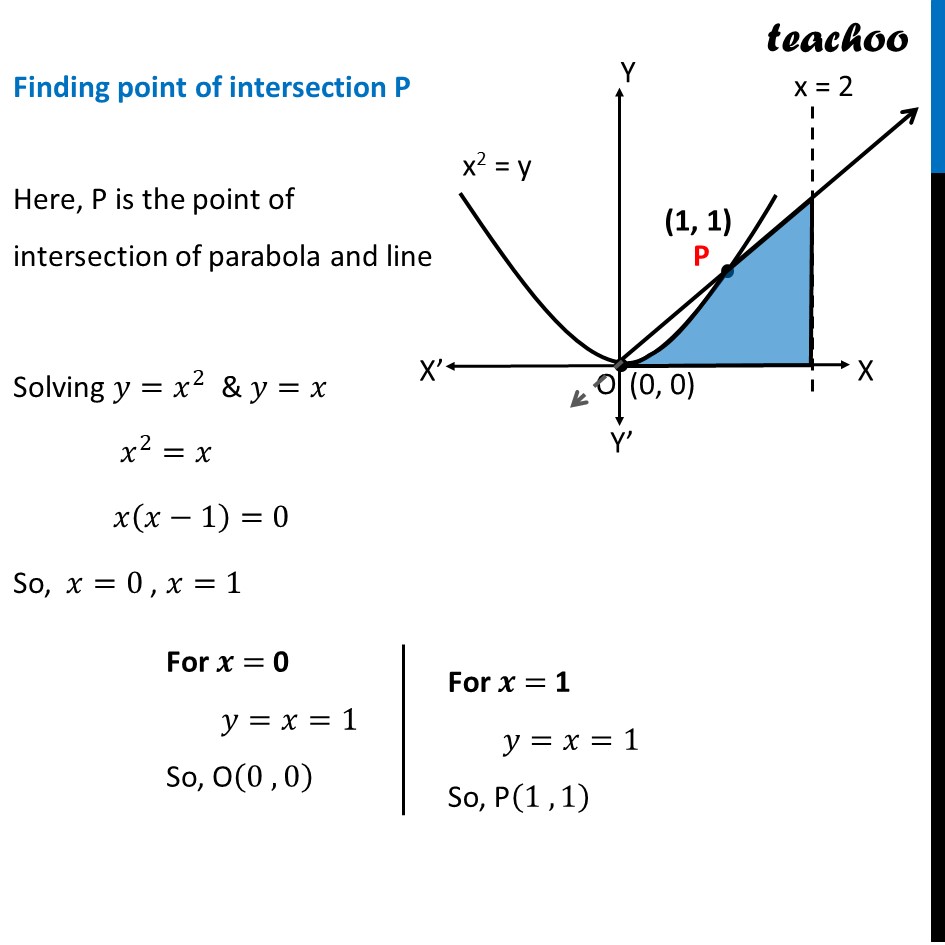
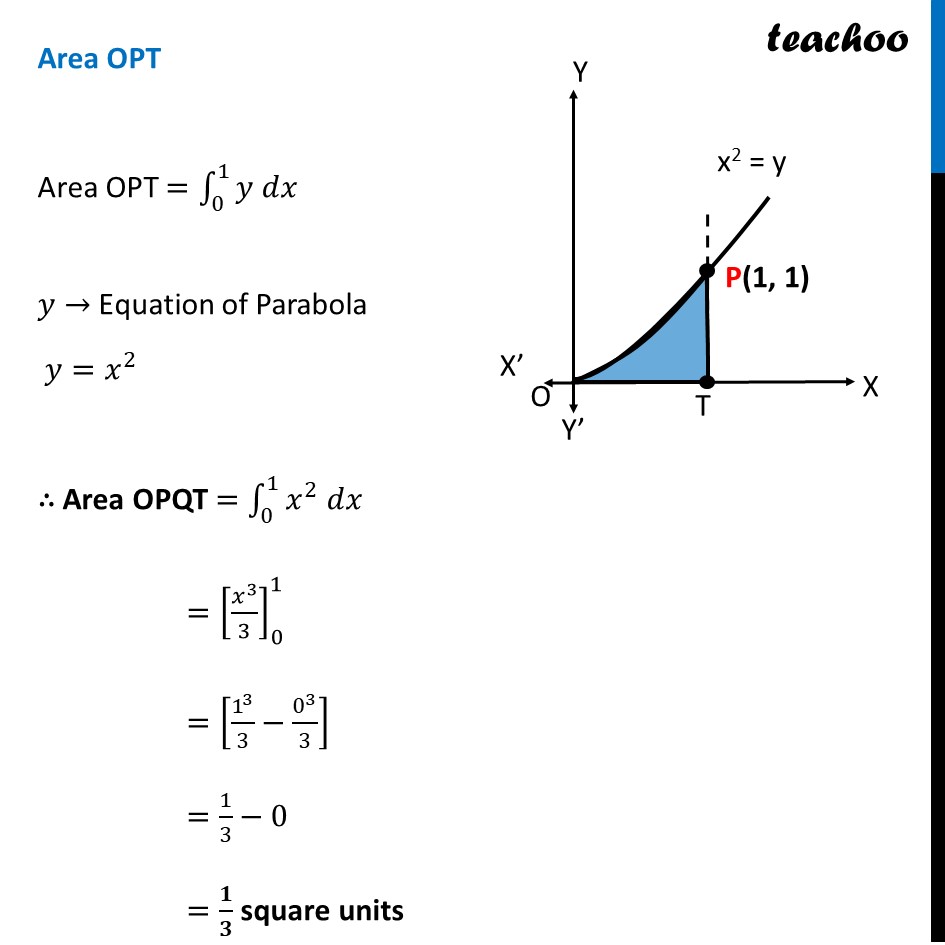
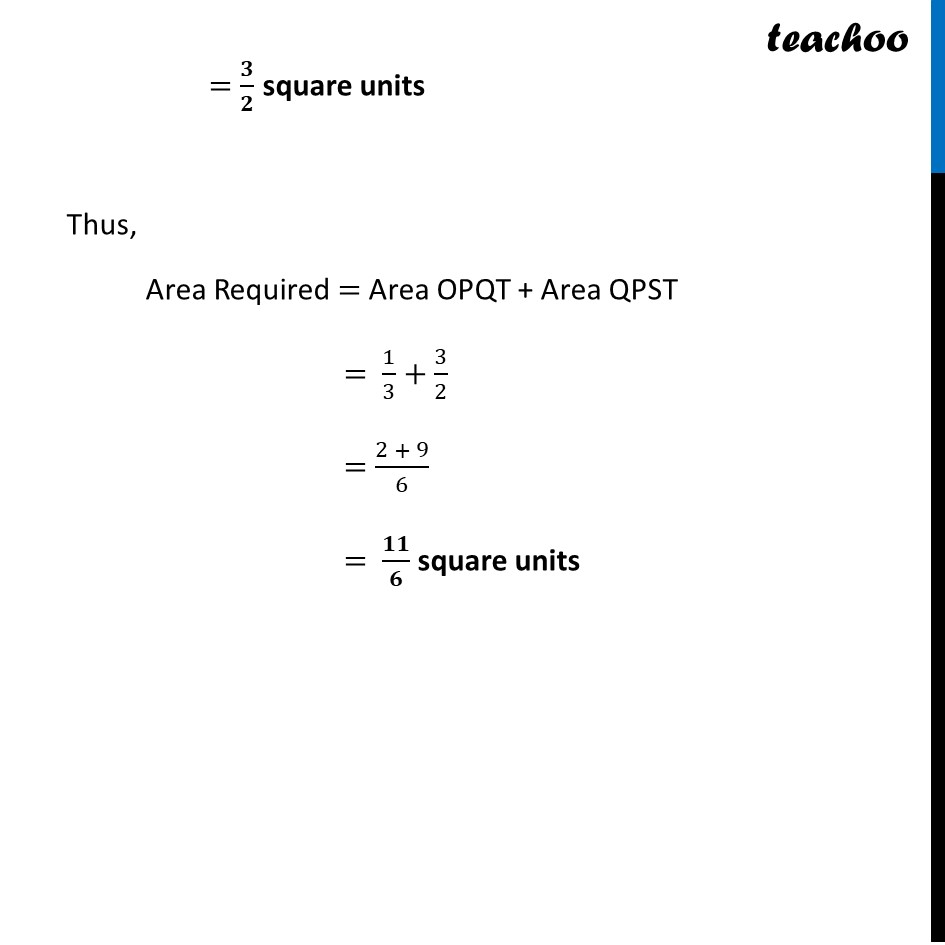
Question 32 Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥^2, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integrationHere, 𝟎≤𝒚≤𝒙^𝟐 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥^2 i.e. 𝑥^2=𝑦 So, it is a parabola 𝟎≤𝒚≤𝒙 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥 It is a straight line Also 𝟎≤𝒙≤𝟐 Since 𝑦≥0 & 0≤𝑥≤2 We work in First quadrant with 0≤𝑥≤2 So, our figure is Finding point of intersection P Here, P is the point of intersection of parabola and line Solving 𝑦=𝑥^2 & 𝑦=𝑥 𝑥^2=𝑥 𝑥(𝑥−1)=0 So, 𝑥=0 , 𝑥=1 For 𝒙 = 0 𝑦=𝑥=1 So, O(0 , 0) For 𝒙 = 1 𝑦=𝑥=1 So, P(1 , 1) Finding area Area required = Area OPQRST Area OPSRQ = Area OPT + Area PQRS Area OPT Area OPT =∫_0^1▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of Parabola 𝑦=𝑥^2 ∴ Area OPQT =∫_0^1▒〖𝑥^2 𝑑𝑥〗 =[𝑥^3/3]_0^1 =[1^3/3−0^3/3] =1/3−0 =𝟏/𝟑 square units Area PQRS Area QRST=∫_1^2▒〖𝑦 𝑑𝑥〗 Here, 𝑦→ equation of line QP 𝑦=𝑥 ∴ Area QRST=∫_1^2▒𝑥 𝑑𝑥 =[𝑥^2/2]_1^2 =[2^2/2−1^2/2] =2−1/2=𝟑/𝟐 square units Thus, Area Required = Area OPQT + Area QPST = 1/3+3/2 = (2 + 9)/6 = 𝟏𝟏/𝟔 square units