Question 4 - CBSE Class 12 Sample Paper for 2023 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Last updated at Dec. 13, 2024 by Teachoo

The value of ‘k’ for which the function f(x)={(1 -cos⁡4x/8x ² ,if x≠0 k,if x=0 is continuous at x = 0 is

(a) 0 (b) -1 (c) 1 (d) 2

$[MCQ] The value of ‘k’ for which function f(x) = { 1 - cos4x / 8x^2 - CBSE Class 12 Sample Paper for 2023 Boards$

part 2 - Question 4 - CBSE Class 12 Sample Paper for 2023 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards - Class 12

part 3 - Question 4 - CBSE Class 12 Sample Paper for 2023 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards - Class 12

Next: Question 5 → Share on WhatsApp

Transcript

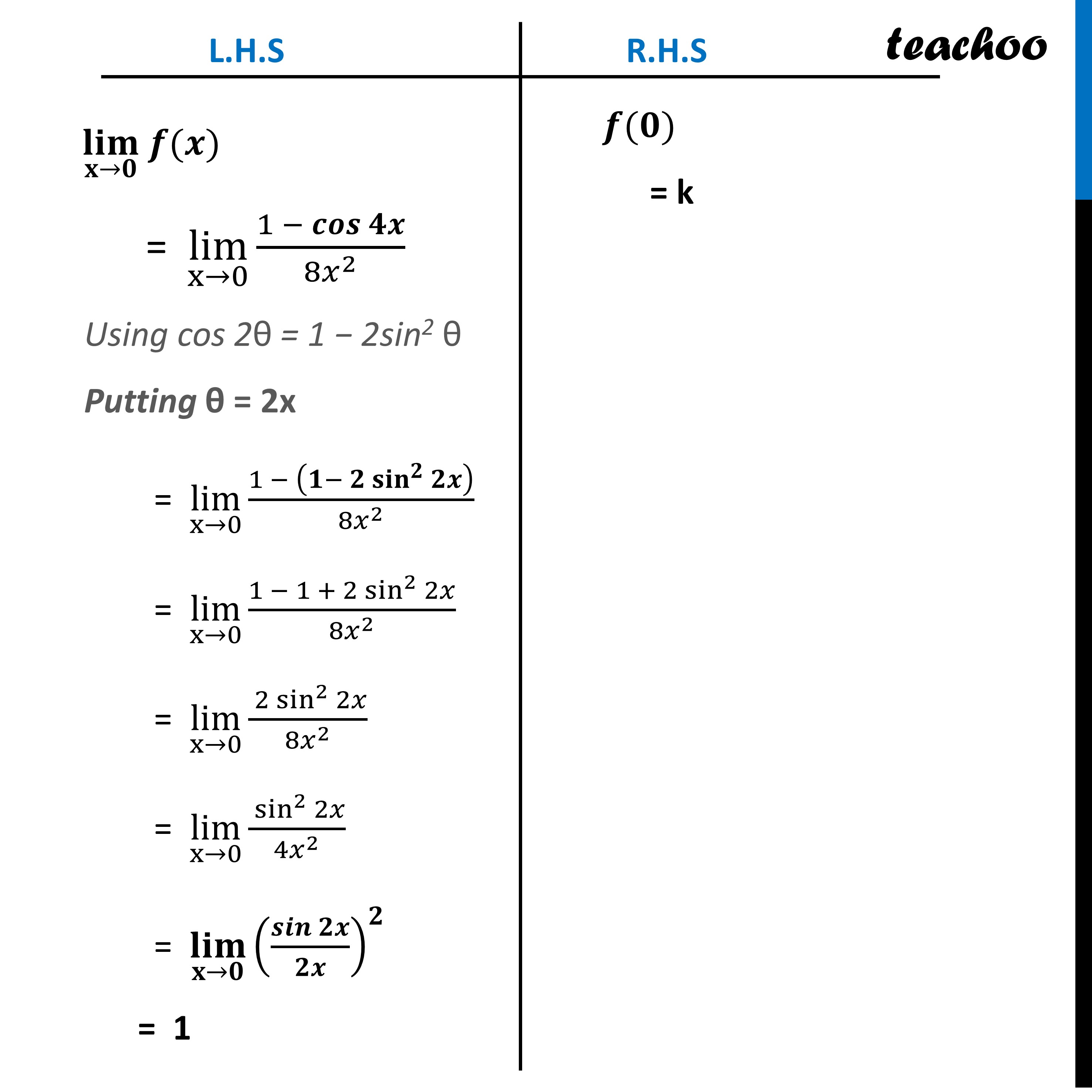
Question 4 The value of ‘k’ for which the function 𝑓(𝑥)={█((1 −cos⁡4𝑥)/〖8𝑥〗^2 , 𝑖𝑓 𝑥≠0@&𝑘, 𝑖𝑓 𝑥=0)┤ is continuous at x = 0 is (a) 0 (b) -1 (c) 1 (d) 2At 𝒙=𝟎 f(x) is continuous at x = 0 if (𝐥𝐢𝐦)┬(𝐱→𝟎) 𝒇(𝒙) = 𝒇(𝟎) L.H.S (𝐥𝐢𝐦)┬(𝐱→𝟎) 𝒇(𝒙) "= " lim┬(x→0) (1 − 𝒄𝒐𝒔⁡𝟒𝒙)/〖8𝑥〗^2 Using cos 2θ = 1 − 2sin2 θ Putting θ = 2x "= " lim┬(x→0) (1 − (𝟏− 𝟐 〖𝐬𝐢𝐧〗^𝟐⁡𝟐𝒙 ))/〖8𝑥〗^2 "= " lim┬(x→0) (1 − 1 + 2 sin^2⁡2𝑥)/〖8𝑥〗^2 "= " lim┬(x→0) ( 2 sin^2⁡2𝑥)/〖8𝑥〗^2 "= " lim┬(x→0) ( sin^2⁡2𝑥)/〖4𝑥〗^2 "= " (𝐥𝐢𝐦)┬(𝐱→𝟎) (𝒔𝒊𝒏⁡𝟐𝒙/𝟐𝒙)^𝟐 = 1 R.H.S 𝒇(𝟎) = k Since f(x) is continuous at x = 0. 1 = k k = 1 So, the correct answer is (c)

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular