Ex 12.2, 5 - Chapter 12 Class 10 Surface Areas and Volumes

Transcript

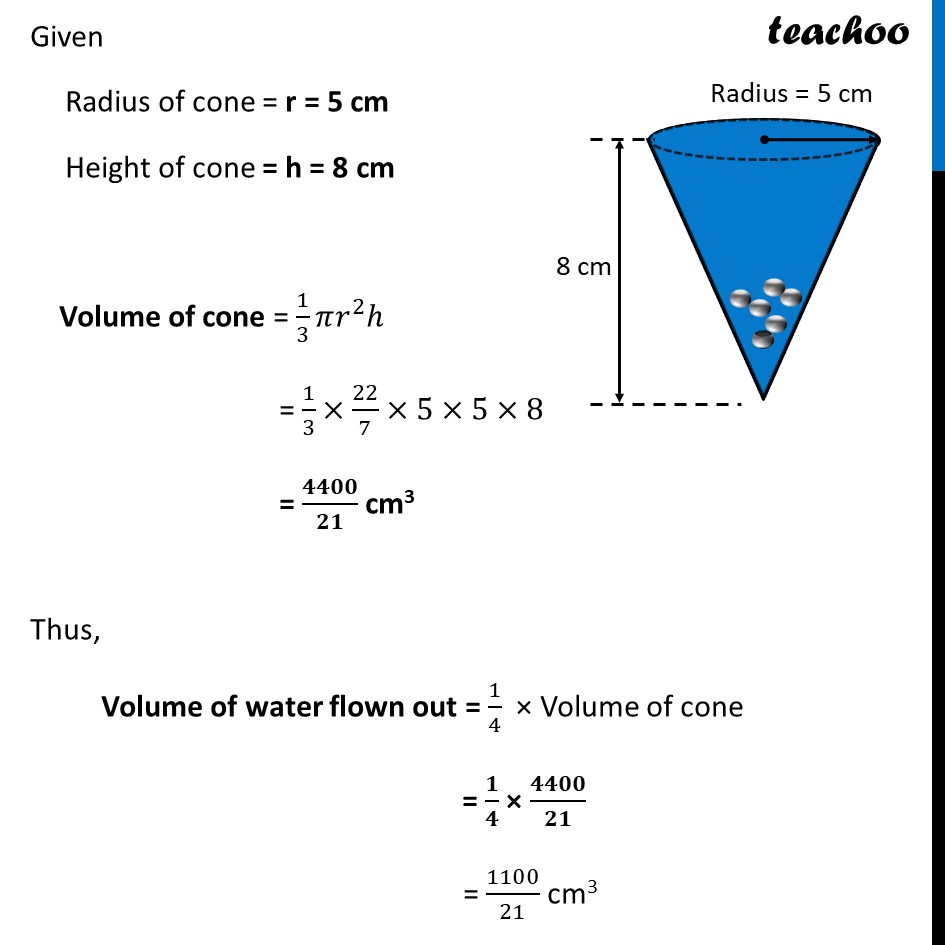
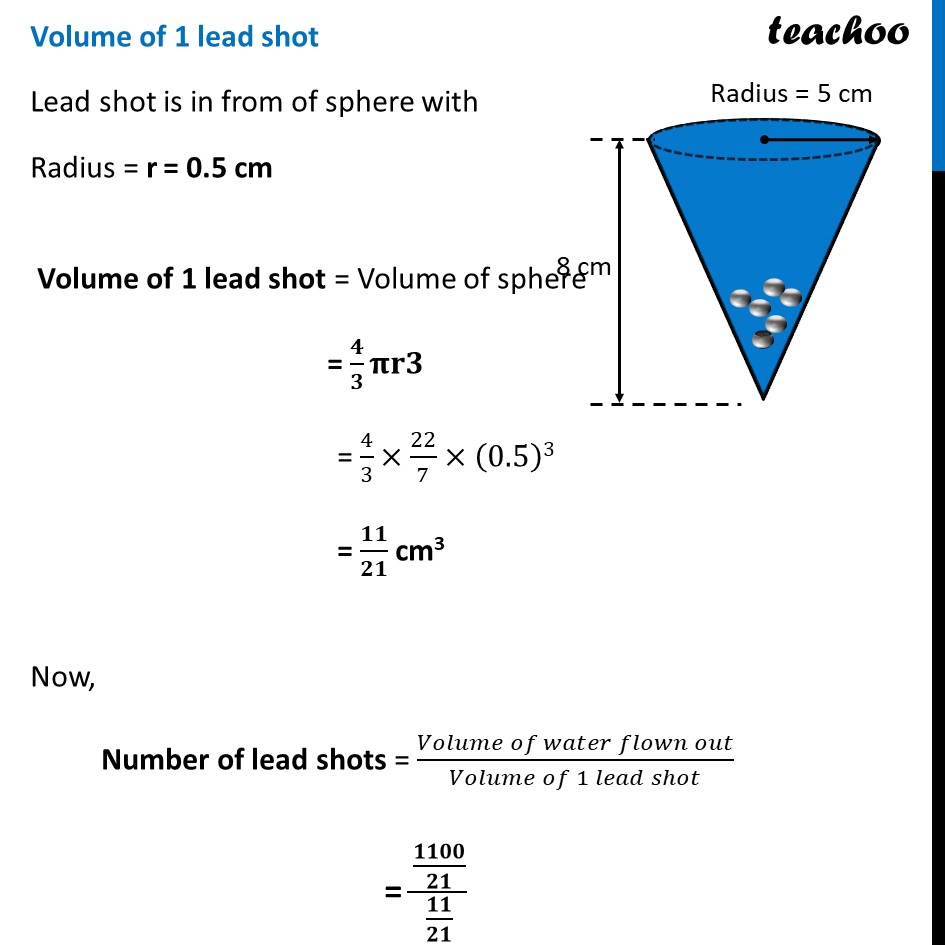
Ex 12.2, 5 A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel. Number of lead shots = (𝑽𝒐𝒍𝒖𝒎𝒆 𝒐𝒇 𝒘𝒂𝒕𝒆𝒓 𝒇𝒍𝒐𝒘𝒏 𝒐𝒖𝒕)/(𝑽𝒐𝒍𝒖𝒎𝒆 𝒐𝒇 𝟏 𝒍𝒆𝒂𝒅 𝒔𝒉𝒐𝒕) Volume of water flown out Volume of water flown out = 𝟏/𝟒 × Volume of cone Given Radius of cone = r = 5 cm Height of cone = h = 8 cm Volume of cone = 1/3 𝜋𝑟^2 ℎ = 1/3×22/7×5×5×8 = 𝟒𝟒𝟎𝟎/𝟐𝟏 cm3 Thus, Volume of water flown out = 1/4 × Volume of cone = 𝟏/𝟒 × 𝟒𝟒𝟎𝟎/𝟐𝟏 = 1100/21 cm3 Volume of 1 lead shot Lead shot is in from of sphere with Radius = r = 0.5 cm Volume of 1 lead shot = Volume of sphere = 𝟒/𝟑 𝛑𝐫𝟑 = 4/3×22/7×(0.5)3 = 𝟏𝟏/𝟐𝟏 cm3 Now, Number of lead shots = (𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑤𝑎𝑡𝑒𝑟 𝑓𝑙𝑜𝑤𝑛 𝑜𝑢𝑡)/(𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 1 𝑙𝑒𝑎𝑑 𝑠ℎ𝑜𝑡) = (𝟏𝟏𝟎𝟎/𝟐𝟏)/(𝟏𝟏/𝟐𝟏) = 1100/21 × 21/11 = 100 Hence there are 100 such lead shots.