Example 1 - Chapter 11 Class 10 Areas related to Circles

Transcript

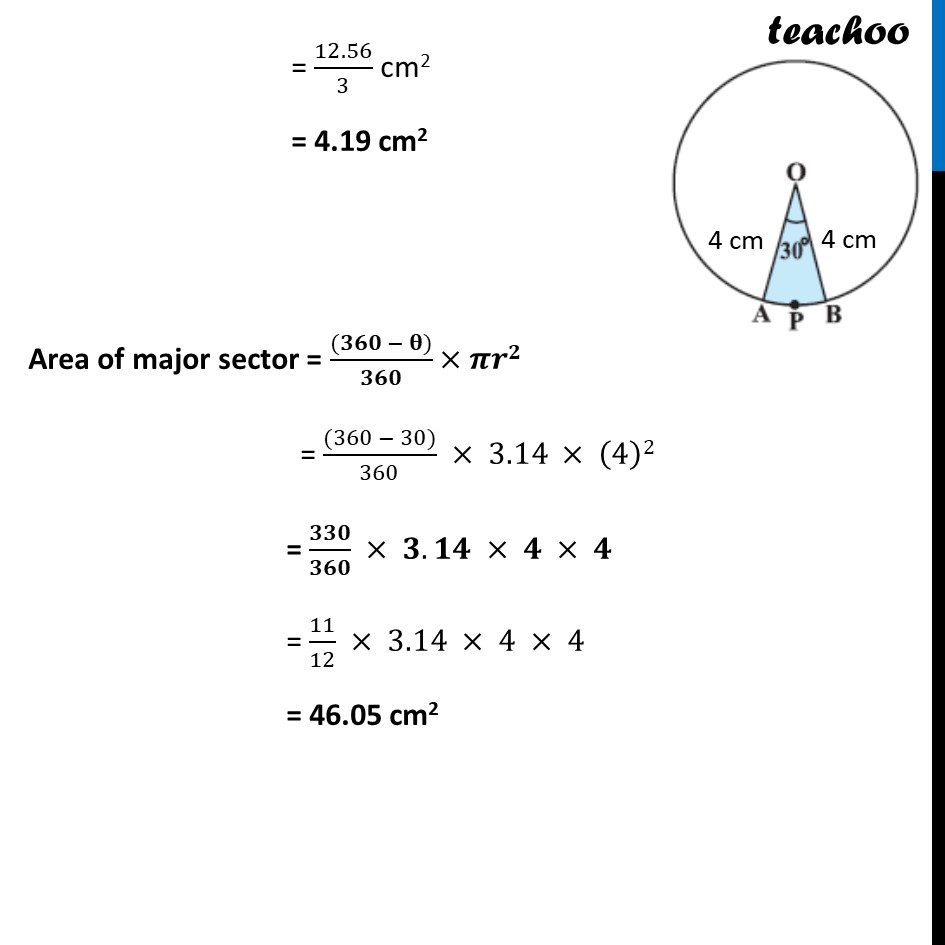
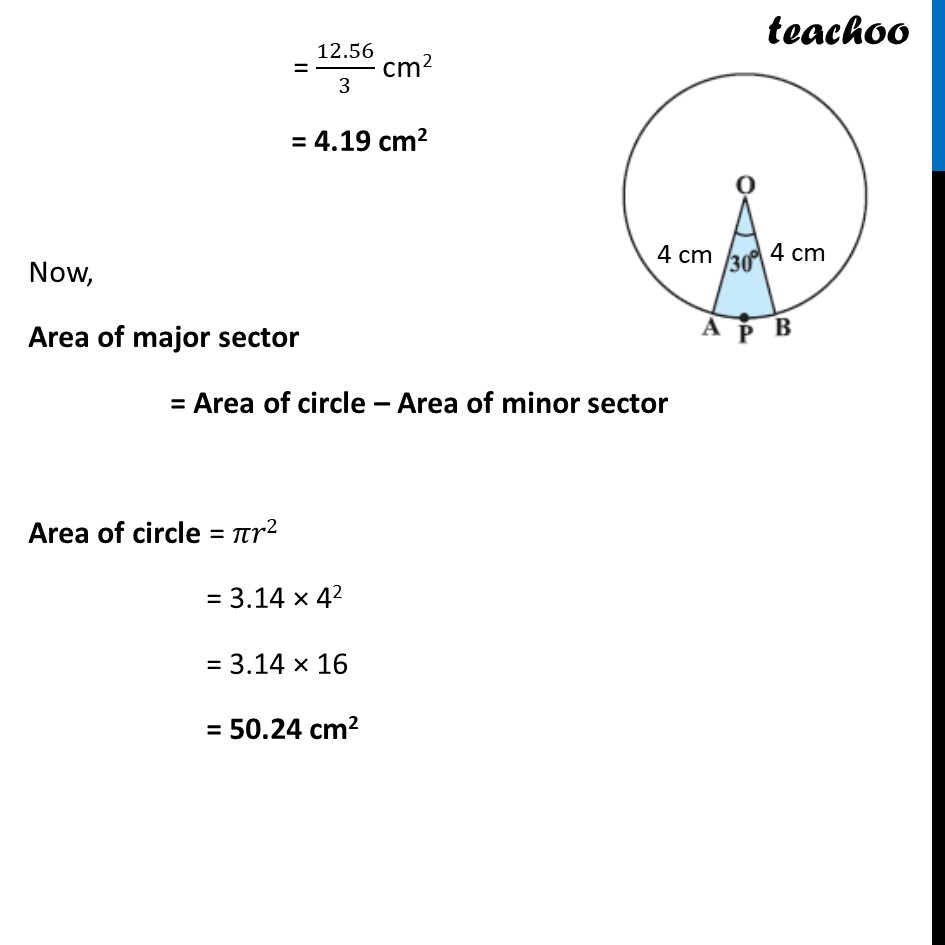
Example 1 (Method 1) Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14). Here, radius = r = 4 cm, θ=30° Now, Area of sector = 𝜃/360×𝜋𝑟2 = 30/360×3.14×(4)2 = 1/12×3.14×4×4 = 1/3×3.14×4 = 12.56/3 cm2 = 4.19 cm2 Area of major sector = ((360 − θ))/360×𝜋𝑟2 = ((360 − 30))/360×3.14×(4)2 = 330/360×3.14×4×4 = 11/12×3.14×4×4 = 46.05 cm2 Example 1 (Method 2) Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π= 3.14). Here, radius = r = 4 cm, θ=30° Now, Area of sector = 𝜃/360×𝜋𝑟2 = 30/360×3.14×(4)2 = 1/12×3.14×4×4 = 1/3×3.14×4 = 12.56/3 cm2 = 4.19 cm2 Area of major sector = Area of circle – Area of minor sector Here, radius = r = 4 cm Area of circle = 𝜋𝑟2 = 3.14 × 42 = 3.14 × 16 = 50.24 cm2 Area of major sector = Area of circle – Area of minor sector = 50.24 – 4.19 = 46.05