Ex 11.1, 7 - Chapter 11 Class 10 Areas related to Circles

Transcript

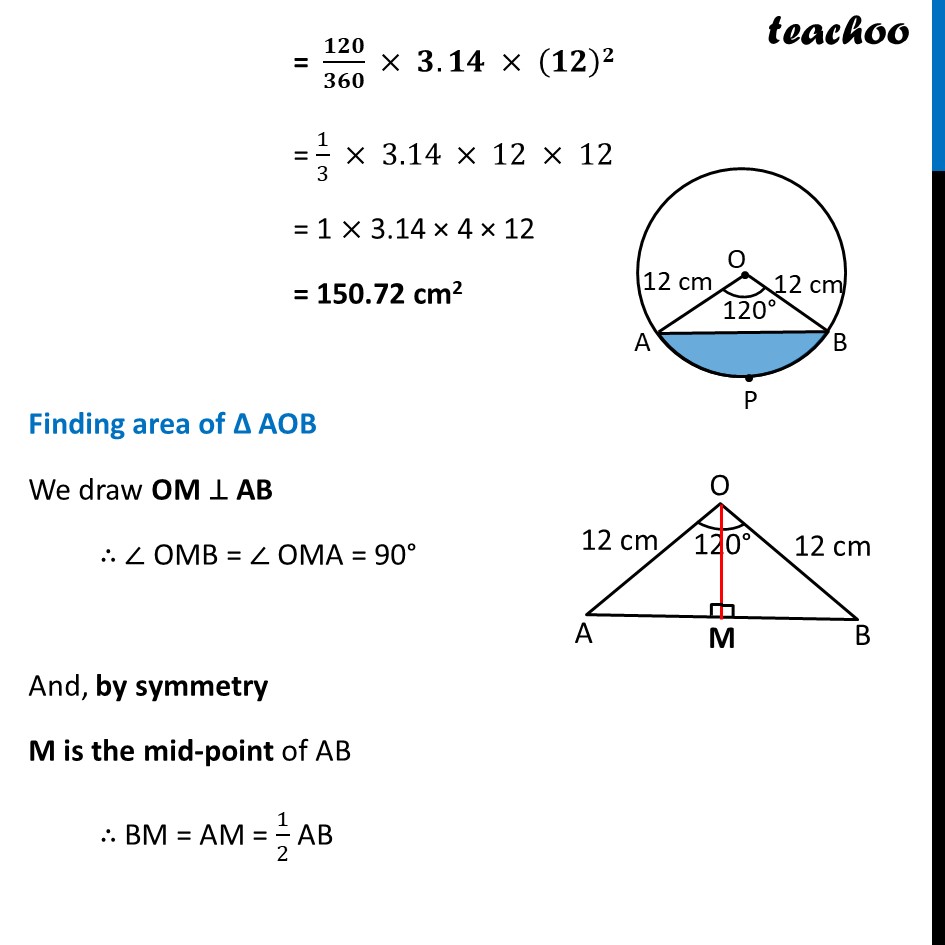
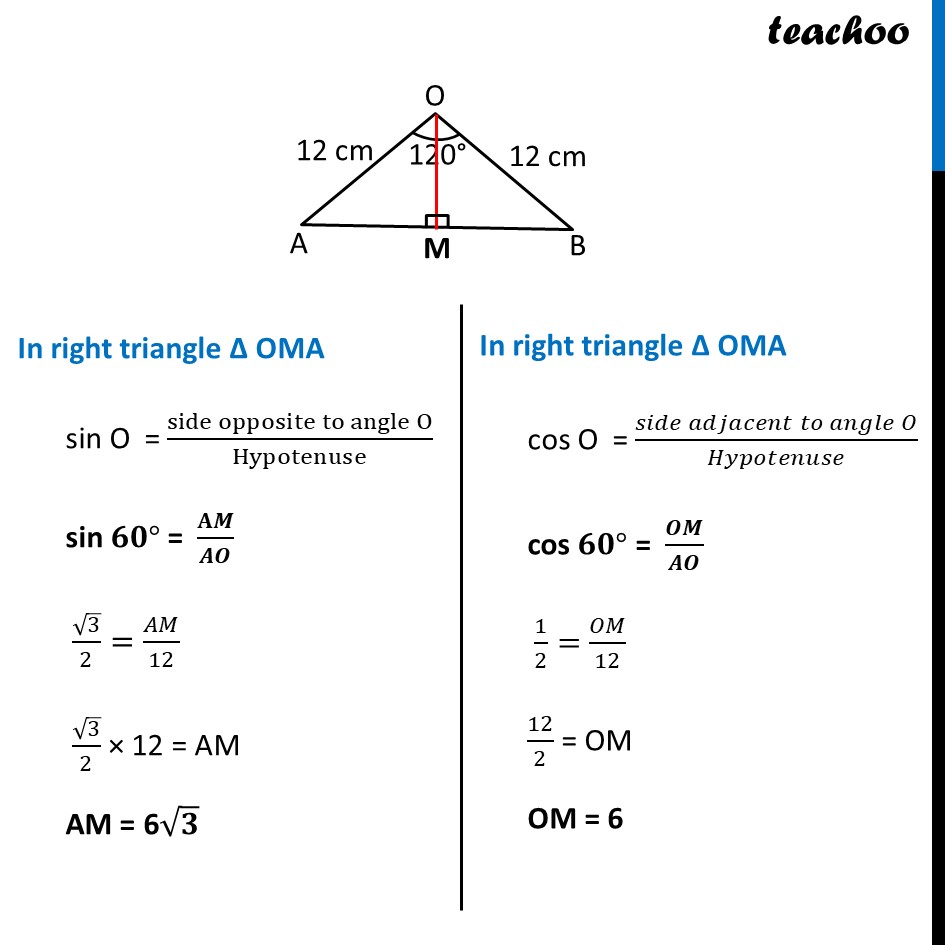
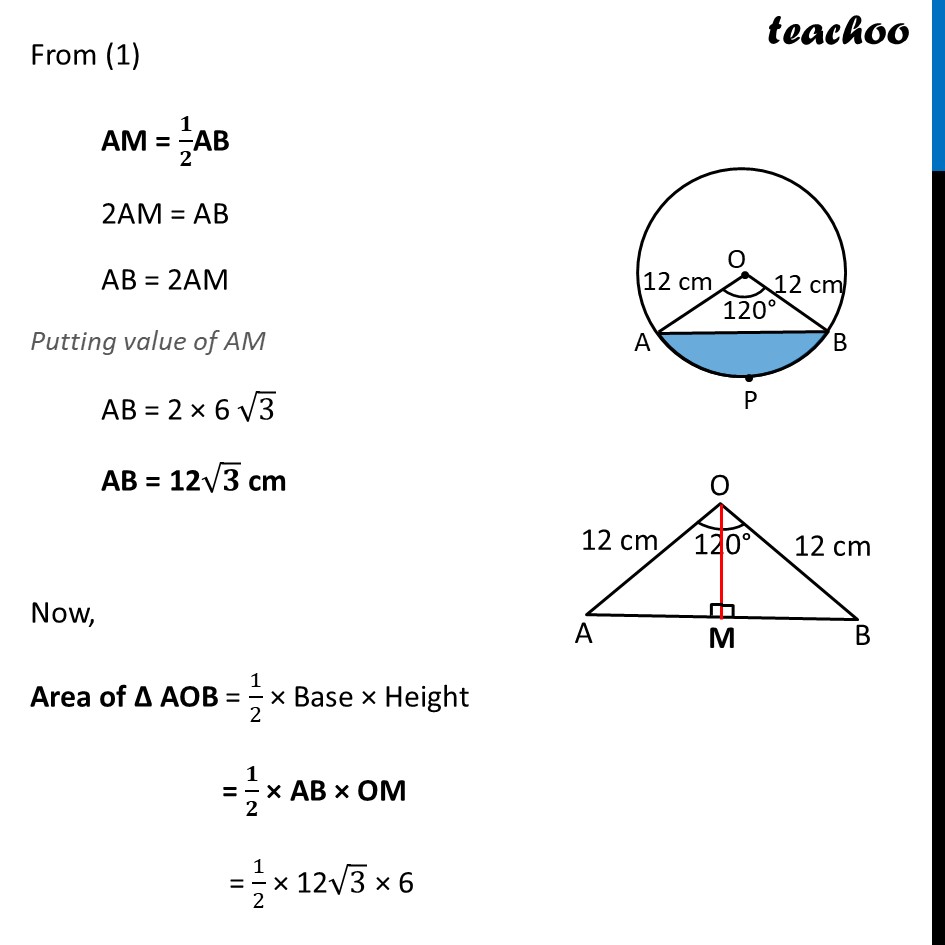
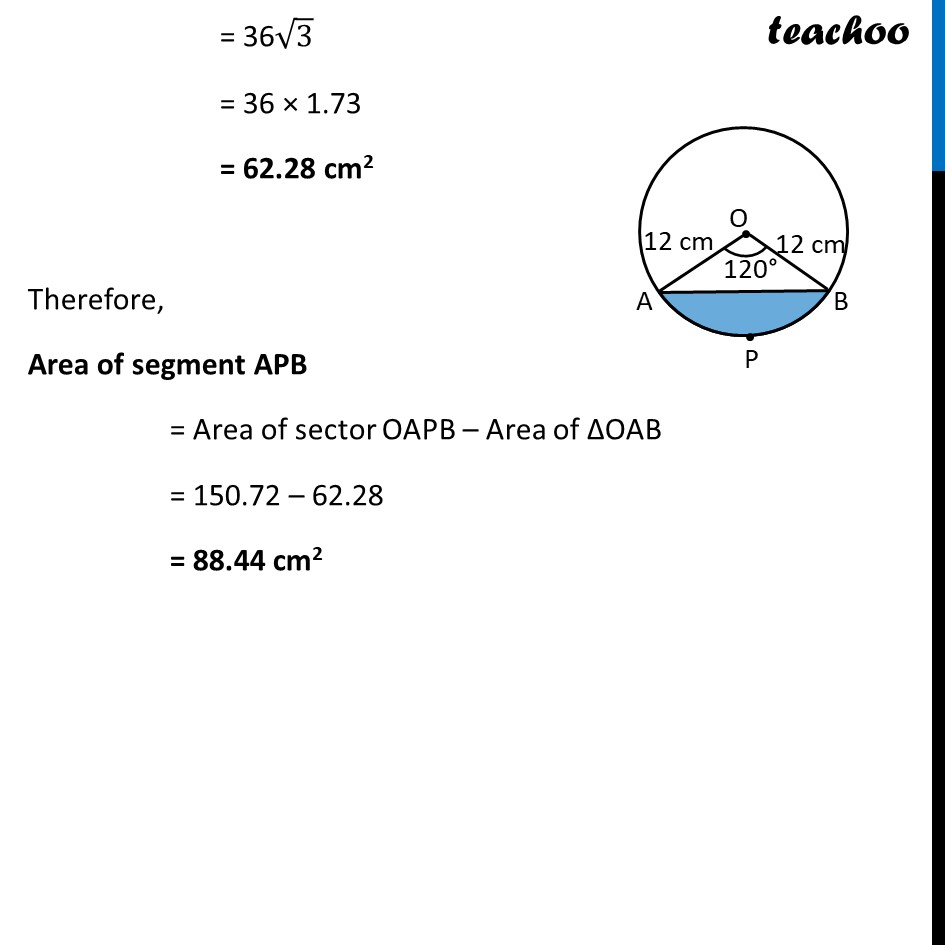
Ex 11.1, 7 A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73) In a given circle, Radius (r) = 12 cm And, 𝜽 = 120° Now, Area of segment APB = Area of sector OAPB – Area of ΔOAB Finding Area of sector OAPB Area of sector OAPB = 𝜃/360× 𝜋𝑟2 = 120/360×3.14×(12)2 = 1/3×3.14×12×12 = 1 × 3.14 × 4 × 12 = 150.72 cm2 Ex 11.1, 7 A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73) In a given circle, Radius (r) = 12 cm And, 𝜽 = 120° Now, Area of segment APB = Area of sector OAPB – Area of ΔOAB Finding Area of sector OAPB Area of sector OAPB = 𝜃/360× 𝜋𝑟2 = 120/360×3.14×(12)2 = 1/3×3.14×12×12 = 1 × 3.14 × 4 × 12 = 150.72 cm2 Finding area of Δ AOB We draw OM ⊥ AB ∴ ∠ OMB = ∠ OMA = 90° And, by symmetry M is the mid-point of AB ∴ BM = AM = 1/2 AB In right triangle Δ OMA sin O = (side opposite to angle O)/Hypotenuse sin 𝟔𝟎° = 𝐀𝑴/𝑨𝑶 √3/2=𝐴𝑀/12 √3/2 × 12 = AM AM = 6√𝟑 In right triangle Δ OMA cos O = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑂)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 cos 𝟔𝟎° = 𝑶𝑴/𝑨𝑶 1/2=𝑂𝑀/12 12/2 = OM OM = 6 From (1) AM = 𝟏/𝟐AB 2AM = AB AB = 2AM Putting value of AM AB = 2 × 6 √3 AB = 12√𝟑 cm Now, Area of Δ AOB = 1/2 × Base × Height = 𝟏/𝟐 × AB × OM = 1/2 × 12√3 × 6 = 36√3 = 36 × 1.73 = 62.28 cm2 Therefore, Area of segment APB = Area of sector OAPB – Area of ΔOAB = 150.72 – 62.28 = 88.44 cm2