Ex 11.1, 4 - Chapter 11 Class 10 Areas related to Circles

Transcript

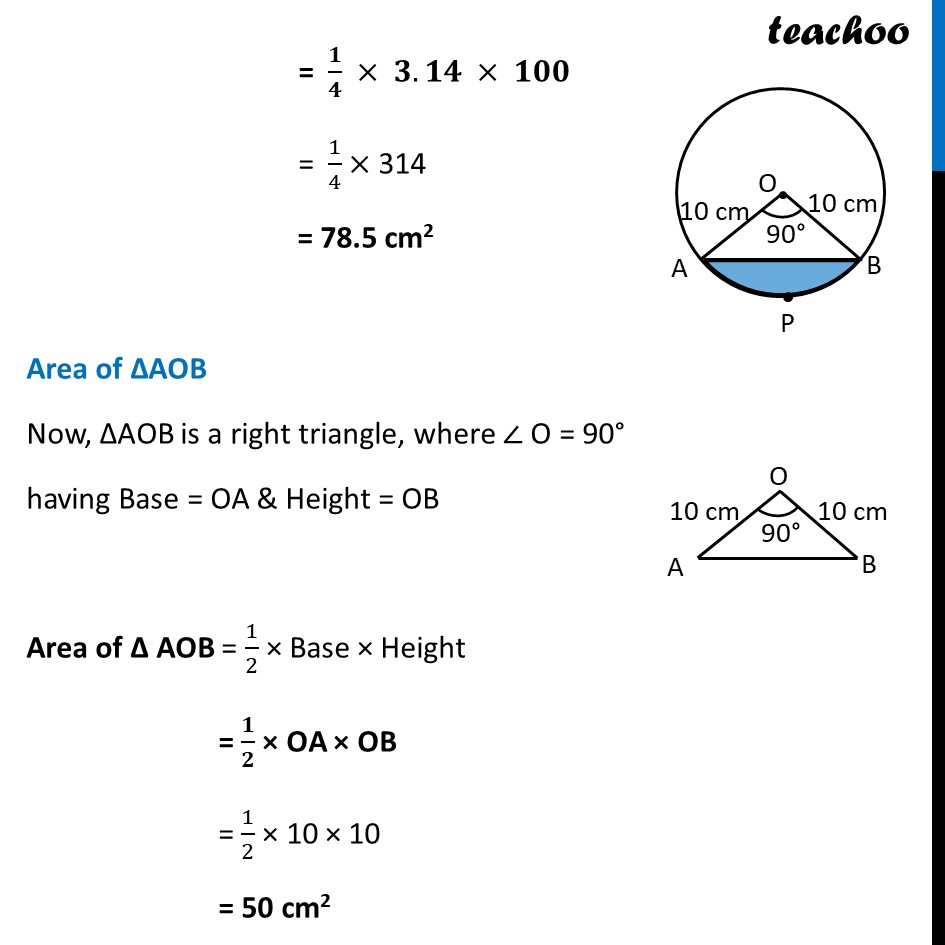
Ex 11.1, 4 A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : minor segment (Use π= 3.14) Given that OA = OB = radius = 10 cm θ=90° Now, Area of segment APB = Area of sector OAPB – Area of ΔAOB Area of sector OAPB Area of sector OAPB = θ/(360°)× πr2 = 90/360 × 3.14 × (10)2 = 𝟏/𝟒 × 𝟑.𝟏𝟒 × 𝟏𝟎𝟎 = 1/4× 314 = 78.5 cm2 Area of ΔAOB Now, ΔAOB is a right triangle, where ∠ O = 90° having Base = OA & Height = OB Area of Δ AOB = 1/2 × Base × Height = 𝟏/𝟐 × OA × OB = 1/2 × 10 × 10 = 50 cm2 Now, Area of segment APB = Area of sector OAPB – Area of ΔAOB = 78.5 – 50 = 28.5 cm2 Ex 11.1, 4 (Method 1) A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : (ii) major sector (Use π= 3.14) Here, θ = 90° & radius = r = 10 cm Area of major sector = ((𝟑𝟔𝟎° − 𝜽))/(𝟑𝟔𝟎°)×𝛑𝐫𝟐 = ((360 − 90))/360 × 3.14 × (10)2 = 𝟐𝟕𝟎/𝟑𝟔𝟎 × 𝟑.𝟏𝟒 × 𝟏𝟎𝟎 = 3/4× 314 = 235.5 cm2 Ex 11.1, 4(Method 2) A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : (ii) major sector (Use π= 3.14) Area of major sector = Area of circle – Area of sector OAPB Area of circle = πr2 = 3.14 × (10)2 = 3.14 × 100 = 314 cm2 Now, Area of major sector = Area of circle – Area of sector OAPB = 314 – 78.5 = 235.5 cm2