Ex 10.2, 9 - Chapter 10 Class 10 Circles (Important Question)

Transcript

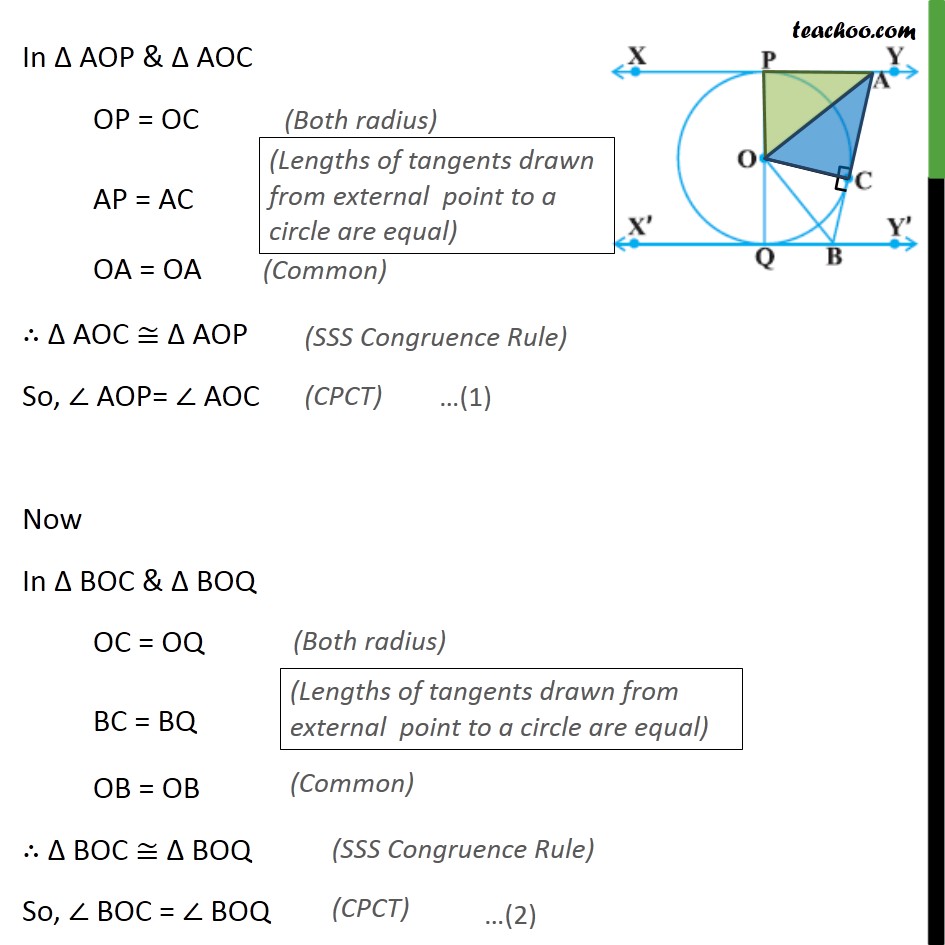
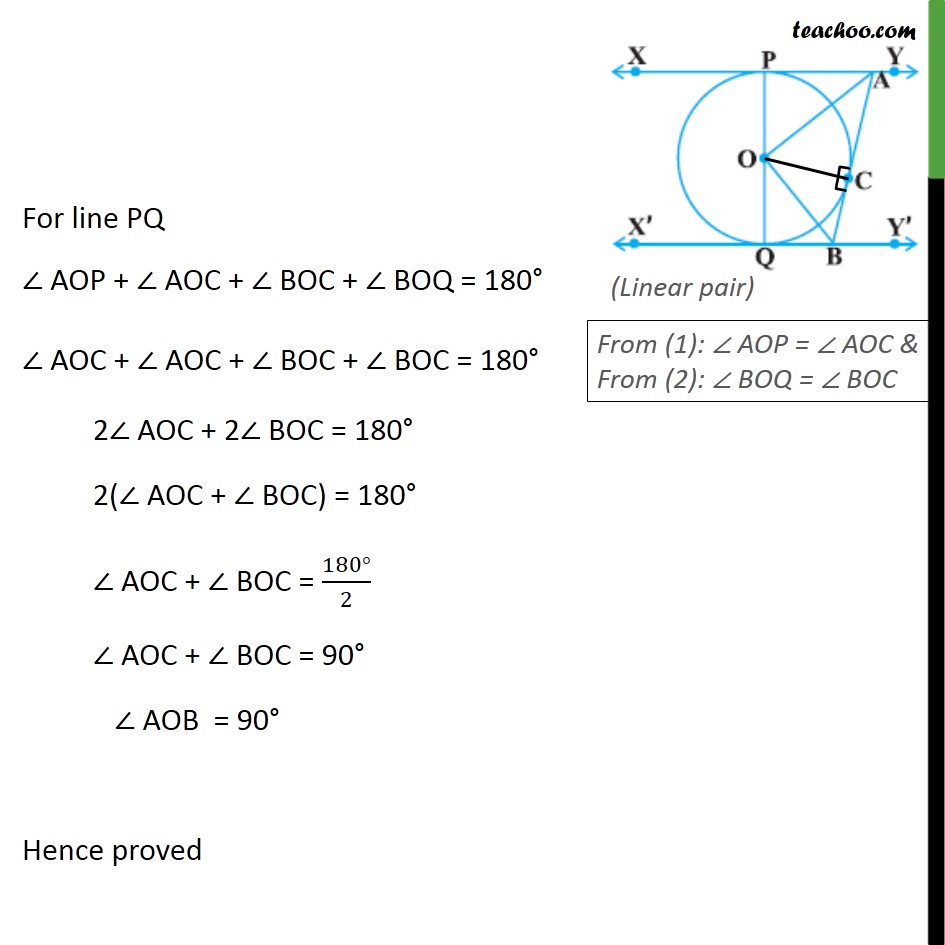
Ex 10.2,9 In figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′at B. Prove that ∠AOB = 90°. Given : XY is a tangent at point P and X’Y’ is a tangent at point Q And XY ∥ X’Y’ AB is a tangent at point C To prove: ∠ AOB = 90° Proof: Join OC For tangent AB & Radius OC OC ⊥ AB So, ∠ ACO = ∠ BCO = 90° In Δ AOP & Δ AOC OP = OC AP = AC OA = OA ∴ Δ AOC ≅ Δ AOP So, ∠ AOP= ∠ AOC Now In Δ BOC & Δ BOQ OC = OQ BC = BQ OB = OB ∴ Δ BOC ≅ Δ BOQ So, ∠ BOC = ∠ BOQ For line PQ ∠ AOP + ∠ AOC + ∠ BOC + ∠ BOQ = 180° ∠ AOC + ∠ AOC + ∠ BOC + ∠ BOC = 180° 2∠ AOC + 2∠ BOC = 180° 2(∠ AOC + ∠ BOC) = 180° ∠ AOC + ∠ BOC = (180°)/2 ∠ AOC + ∠ BOC = 90° ∠ AOB = 90° Hence proved