You are here
Example 10 - Chapter 8 Class 10 Introduction to Trignometry
Last updated at Dec. 13, 2024 by Teachoo
Transcript
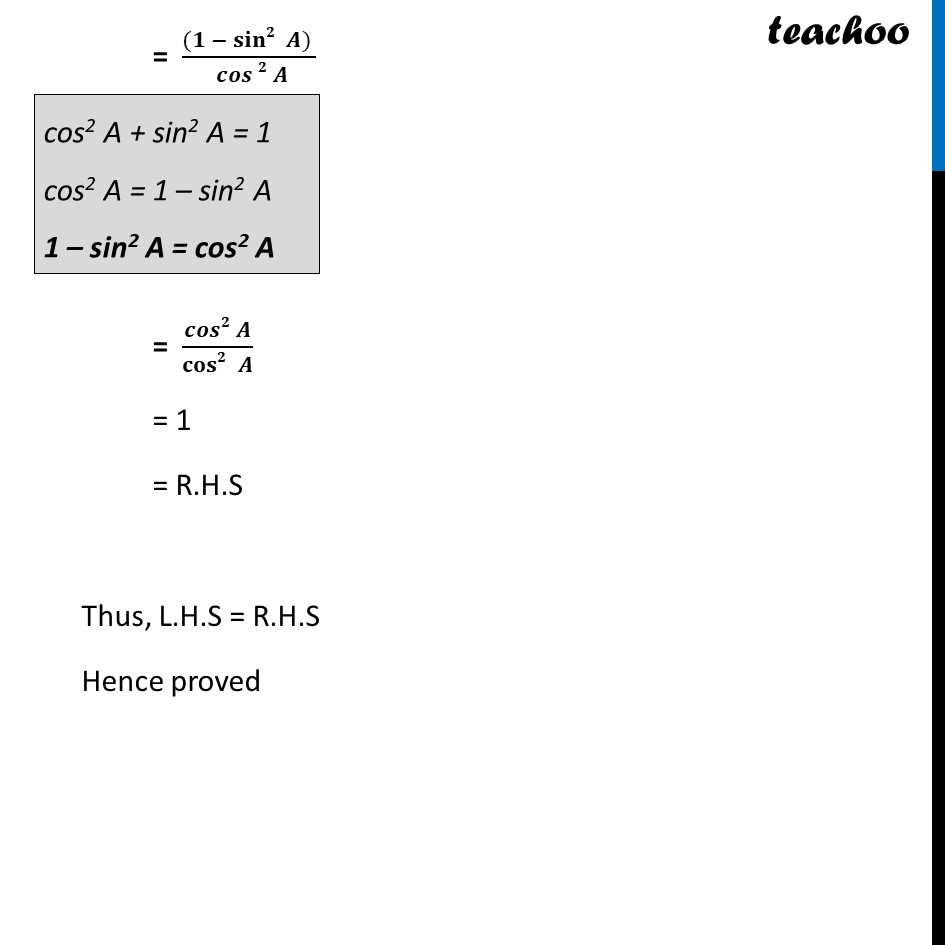
Example 10 Prove that sec A (1 β sin A)(sec A + tan A) = 1. Solving L.H.S sec A (1 β sin A) (sec A + tan A) Writing everything in terms of sin A and cos A = 1/cosβ‘γ π΄γ (1 β sin A) (" " 1/cosβ‘γ π΄γ +" " sinβ‘γ π΄γ/cosβ‘γ π΄γ ) = ((1 βγ sinγβ‘γ π΄)γ)/(cosβ‘ π΄) (" " (1 +γ sinγβ‘γ π΄γ)/cosβ‘γ π΄γ ) = ((π βγ πππγβ‘γ π¨) (π+γ πππγβ‘γ π¨)γ γ)/(πππβ‘ π¨ Γ πππβ‘γ π¨γ ) Since (a β b) (a + b) = a2 β b2 = ((12 βγ sin2γβ‘γ π΄) γ)/( cosβ‘γ2 π΄γ ) = ((π βγ π¬π’π§πγβ‘γ π¨) γ)/( πππβ‘γπ π¨γ ) = (ππππ π¨)/(ππ¨π¬πβ‘ π¨) = 1 = R.H.S Thus, L.H.S = R.H.S Hence proved cos2 A + sin2 A = 1 cos2 A = 1 β sin2 A 1 β sin2 A = cos2 A
