Example 5 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

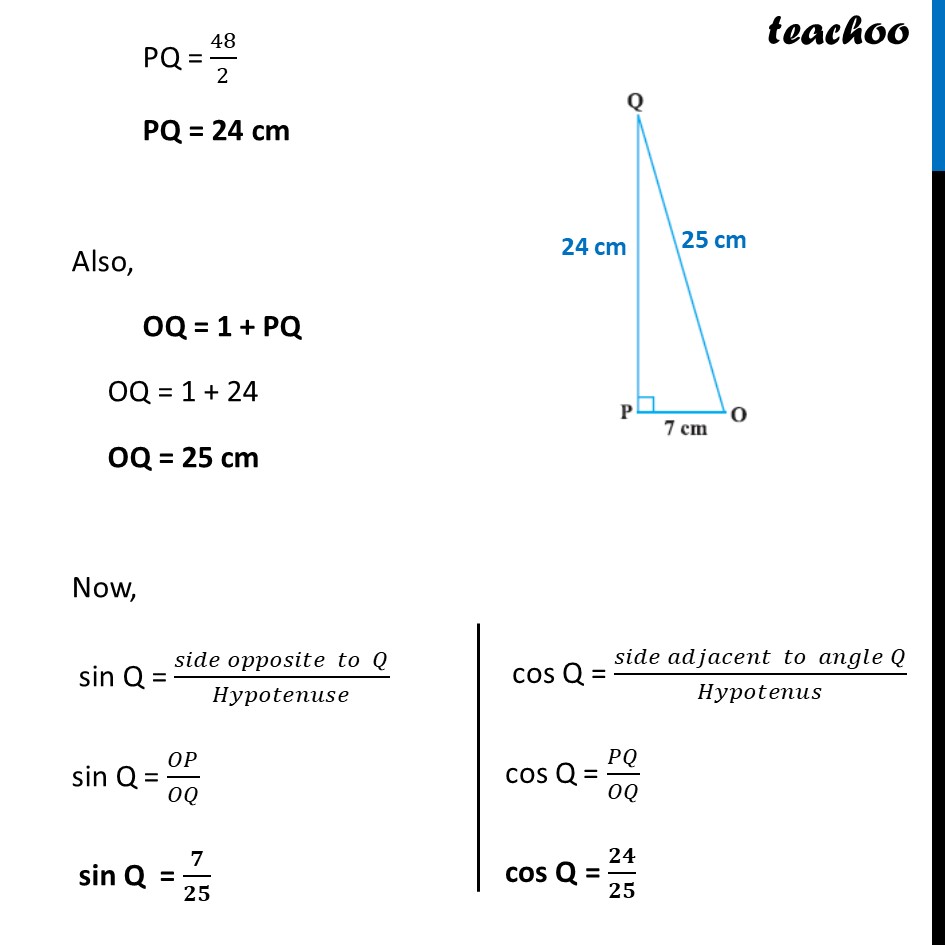
Example 5 In Δ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig.). Determine the values of sin Q and cos Q. Given in Δ OPQ, OQ – PQ = 1 cm OQ = 1 + PQ Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 OQ2 = PQ2 + OP2 (1 + PQ)2 = PQ2 + (7)2 1 + PQ2 + 2PQ = PQ2 + 49 1 + PQ2 + 2PQ – PQ2 – 49 = 0 2PQ – 48 = 0 2PQ = 48 PQ = 48/2 PQ = 24 cm Also, OQ = 1 + PQ OQ = 1 + 24 OQ = 25 cm Now, sin Q = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑄)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 sin Q = 𝑂𝑃/𝑂𝑄 sin Q = 𝟕/𝟐𝟓 cos Q = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑄)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠 cos Q = 𝑃𝑄/𝑂𝑄 cos Q = 𝟐𝟒/𝟐𝟓