Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class
Example 3 - Chapter 8 Class 10 Introduction to Trignometry
Last updated at May 29, 2023 by Teachoo
Finding values of expressions
Chapter 8 Class 10 Introduction to Trignometry
Concept wise
- Finding sin cos tan
- Finding sin cos when sides of a triangle are given
- Finding ratios when other ratios are given
-
Finding values of expressions
- Proving
- Trignometric ratios of Specific Angles - Evaluating
- Trignometric ratios of complementry angles
- Expressing ratios in other ratios
- Evaluating using Trignometric Identities
Transcript
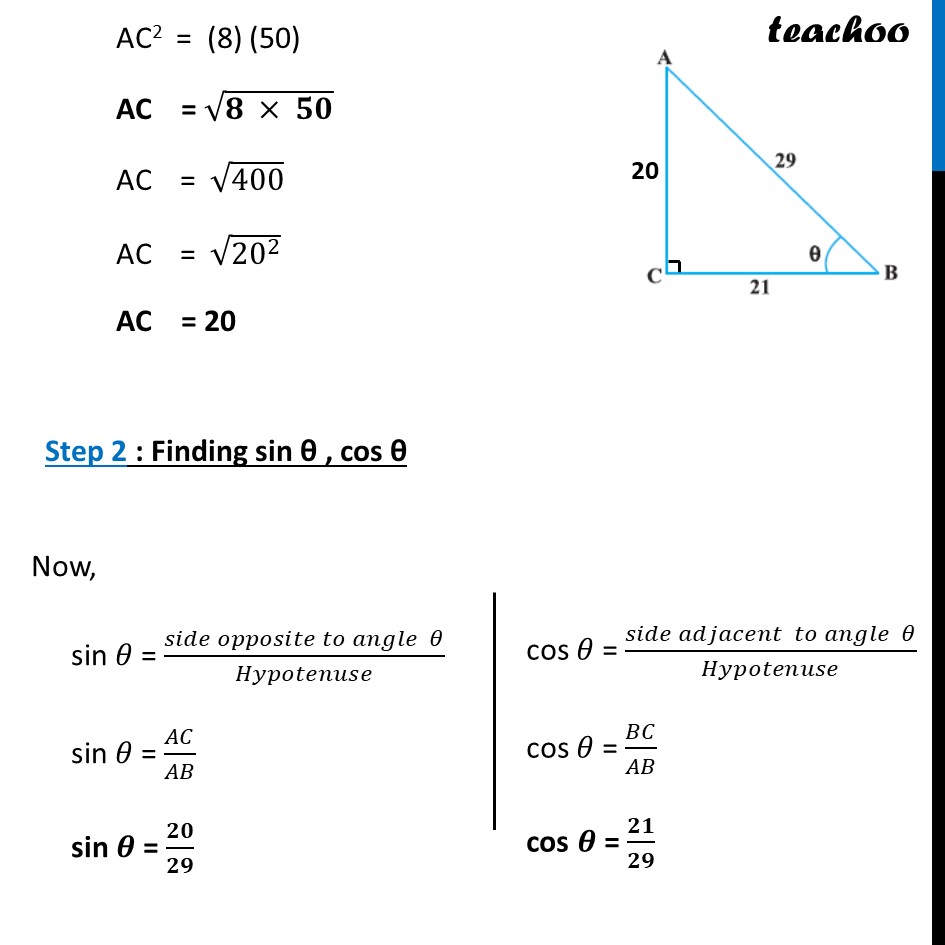
Example 3 Consider ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ABC = (see fig.). Determine the values of (i) cos2 + sin2 , Step1 : Finding sides of triangle In right triangle ABC, using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 AB2 = AC2 + BC2 AC2 = AB2 BC2 AC2 = (29)2 (21)2 Using a2 b2 = (a + b) (a b) AC2 = (29 21) (29 + 21) AC2 = (8) (50) AC = (8 50) AC = 400 AC = 20 Step 2 : Finding sin , cos We have to find out , cos2 + sin2 Putting values = (21/29)^2+(20/29)^2 = ((21)2 + (20)2)/292 = (441 + 400)/841 = 841/841 = 1 So, cos2 + sin2 = 1 Example 3 Consider ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ABC = (see fig.). Determine the values of (ii) cos2 sin2 . cos2 sin2 Putting values = (21/29)^2 (20/29)^2 = ((21)2 (20)2)/292 Using a2 b2 = (a + b) (a b) = ((21 + 20)(21 20))/292 = ((41)(1))/841 = 41/841
