Example 1 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

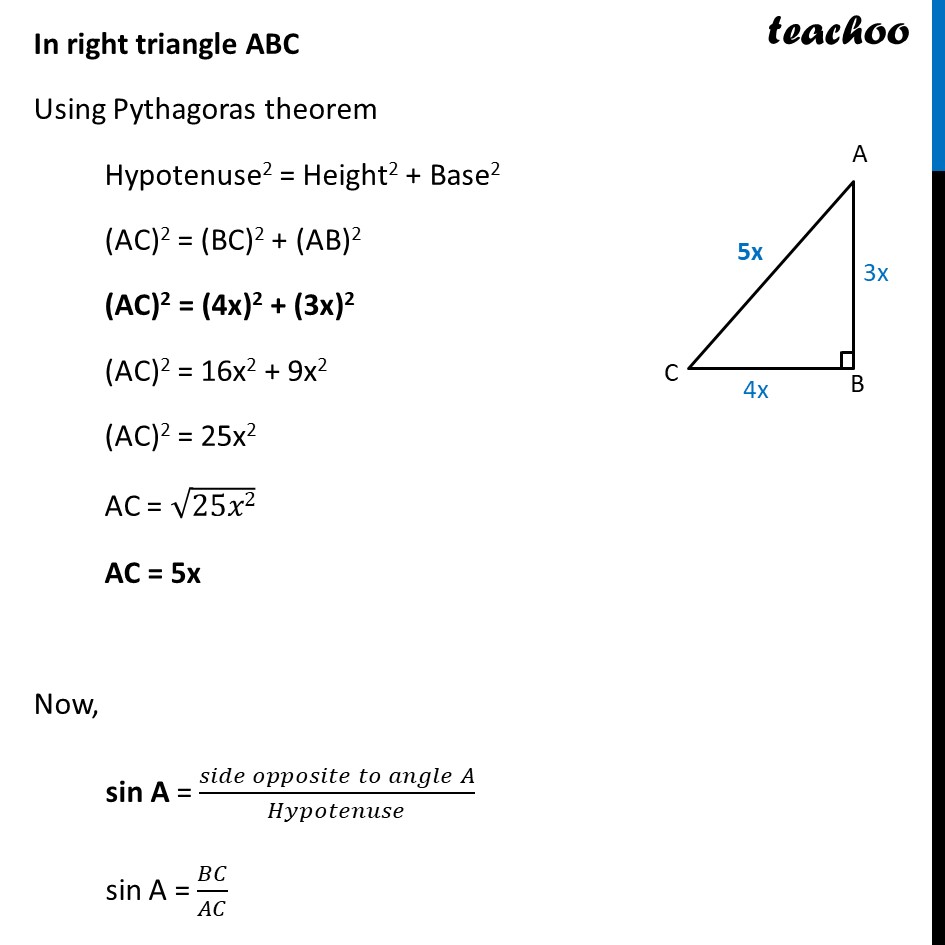
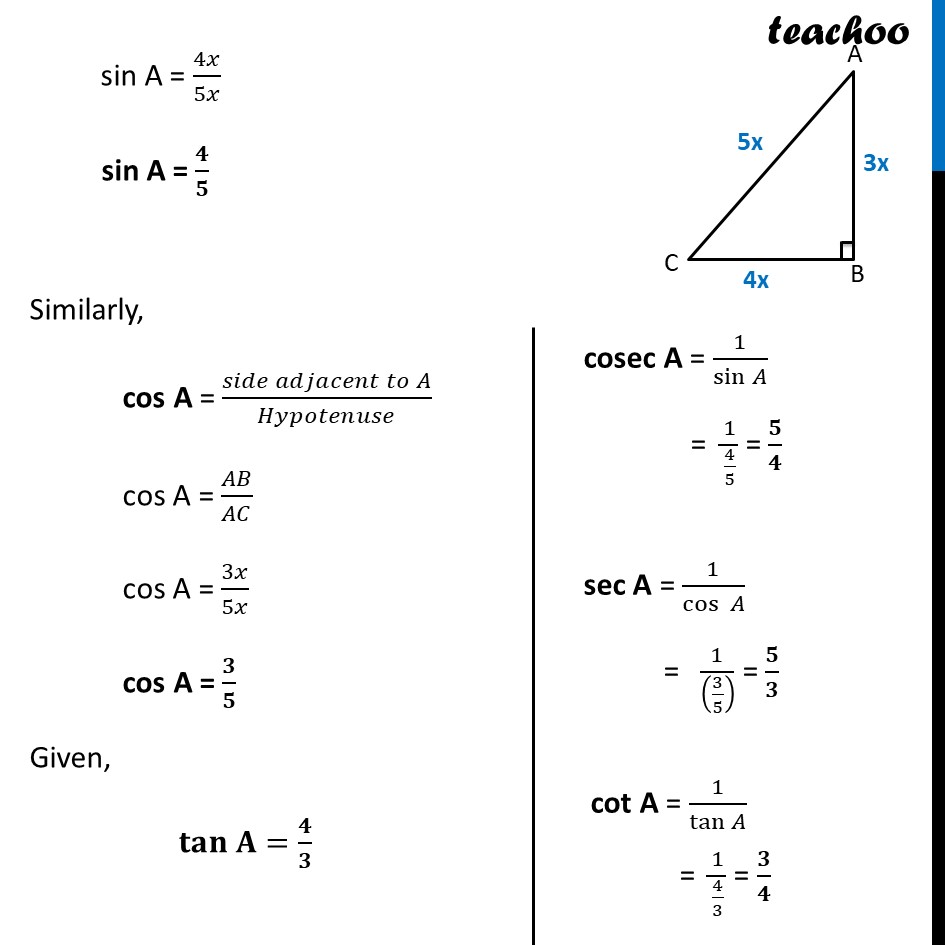
Example 1 Given tan A = 4/3 , find the other trigonometric ratios of the angle A Given, tan A = 4/3 (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝐴)/(𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝐴) = 4/3 𝐵𝐶/𝐴𝐵 = 4/3 Let BC = 4x AB = 3x We find AC using Pythagoras Theorem In right triangle ABC Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (AC)2 = (BC)2 + (AB)2 (AC)2 = (4x)2 + (3x)2 (AC)2 = 16x2 + 9x2 (AC)2 = 25x2 AC = √25𝑥2 AC = 5x Now, sin A = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝐴)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 sin A = 𝐵𝐶/𝐴𝐶 sin A = 4𝑥/5𝑥 Sin A = 4/5 Similarly, cos A = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝐴)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 cos A = 𝐴𝐵/𝐴𝐶 cos A = 3𝑥/5𝑥 cos A = 3/5 Given, tan A=4/3 cosec A = 1/sin⁡𝐴 = 1/(4/5) = 5/4 sec A = 1/cos⁡〖 𝐴〗 = 1/((3/5) ) = 5/3 cot A = 1/tan⁡𝐴 = 1/(4/3) = 3/4