Ex 8.1, 9 - Chapter 8 Class 10 Introduction to Trignometry (Important Question)

Transcript

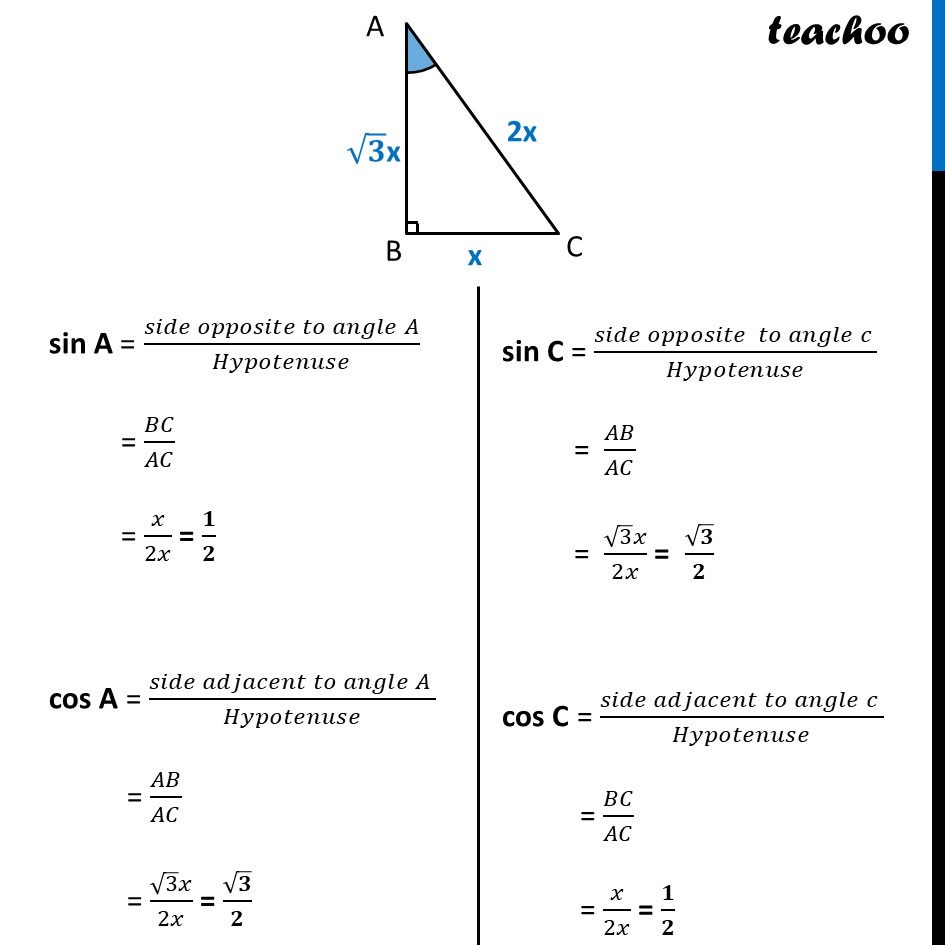
Ex 8.1, 9 In triangle ABC, right-angled at B, if tan A = 1/√3, find the value of sin A cos C + cos A sin C Given tan A = 1/√3 (𝑺𝒊𝒅𝒆 𝒐𝒑𝒑𝒐𝒔𝒊𝒕𝒆 𝒕𝒐 𝑨)/(𝑺𝒊𝒅𝒆 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕 𝒕𝒐 𝑨) = 𝟏/√𝟑 𝐵𝐶/𝐴𝐵 = 1/√3 Let BC = x & AB = √𝟑 x We have to find sin A cos C + cos A sin C Putting sin A = 1/2 , cos A = √3/2 , sin C = √3/2 & cos C = 1/2 = (𝟏/𝟐)×(𝟏/𝟐)+(√𝟑/𝟐)×(√𝟑/𝟐) = 1/4 + (√3 × √3)/4 = 1/4 + 3/4 = (1 + 3)/4 = 4/4 = 1 So, sin A cos C + cos A sin C = 1 Ex 8.1, 9 In triangle ABC, right-angled at B, if tan A = 1/√3, find the value of (ii) cos A cos C – sin A sin C cos A cos C – sin A sin C Putting sin A = 1/2 , cos A = √3/2 , sin C = √3/2 & cos C = 1/2 = (√𝟑/𝟐)×𝟏/𝟐−(𝟏/𝟐)×(√𝟑/𝟐) = (√3/4)−(√3/4) = 0 Hence, cos A cos C – sin A sin C = 0