Ex 8.1, 7 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

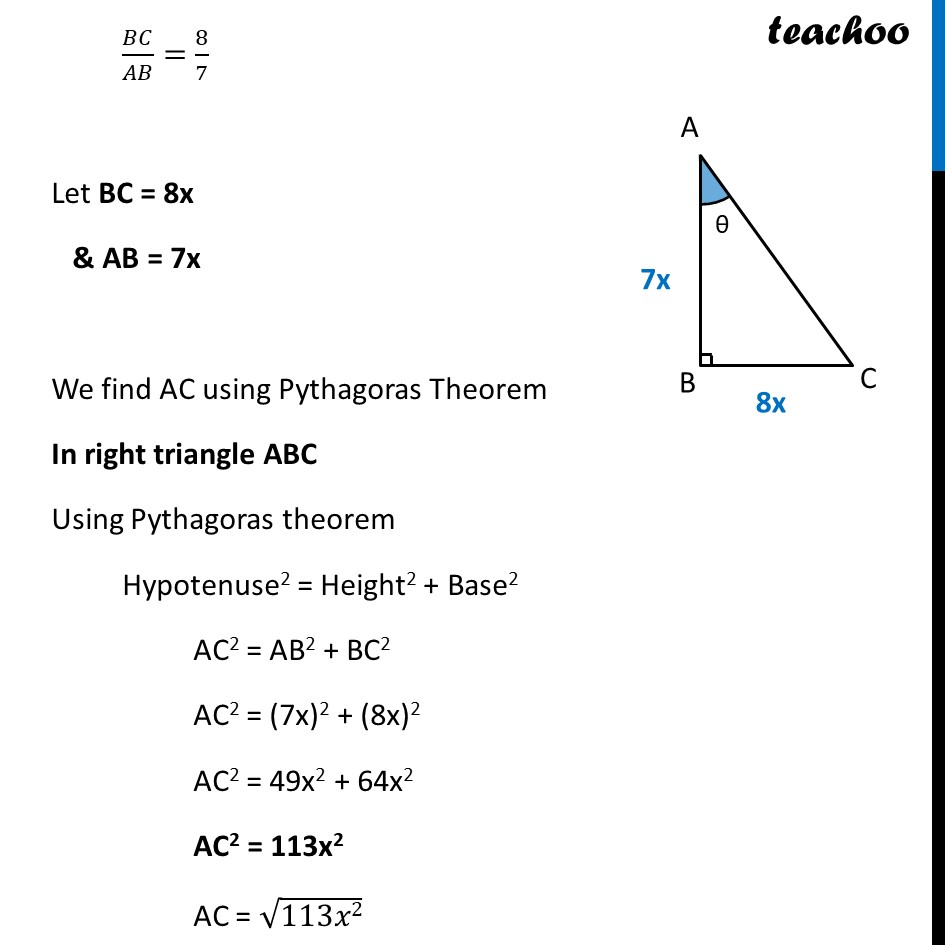
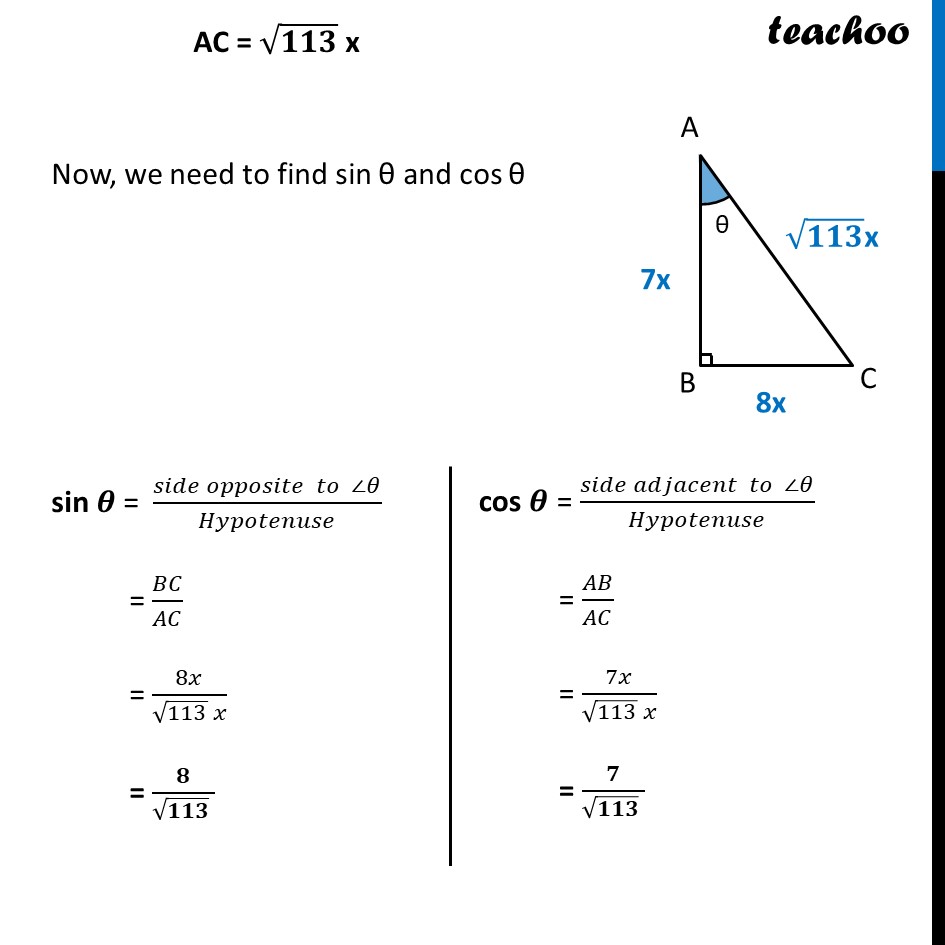
Ex 8.1, 7 If cot θ = 7/8 , evaluate : (i) ((1 + 𝑠𝑖𝑛⁡𝜃)(1 − 𝑠𝑖𝑛⁡𝜃))/((1 + 𝑐𝑜𝑠⁡𝜃)(1 − 𝑐𝑜𝑠⁡𝜃)) We will first calculate the value of sin θ & cos θ Now, tan θ = 1/cot⁡𝜃 tan 𝛉 = 𝟖/𝟕 We can write tan 𝜃 = 8/7 (𝒔𝒊𝒅𝒆 𝒐𝒑𝒑𝒐𝒔𝒊𝒕𝒆 ∠𝜽)/(𝒔𝒊𝒅𝒆 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕 ∠𝜽)=𝟖/𝟕 𝐵𝐶/𝐴𝐵=8/7 Let BC = 8x & AB = 7x We find AC using Pythagoras Theorem In right triangle ABC Using Pythagoras theorem Hypotenuse2 = Height2 + Base2 AC2 = AB2 + BC2 AC2 = (7x)2 + (8x)2 AC2 = 49x2 + 64x2 AC2 = 113x2 AC = √113𝑥2 AC = √𝟏𝟏𝟑 x AC = √𝟏𝟏𝟑 x Now, we need to find sin θ and cos θ sin 𝜽 = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝜃)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝐵𝐶/𝐴𝐶 = 8𝑥/(√113 𝑥) = 𝟖/(√𝟏𝟏𝟑 ) cos 𝜽 = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠𝜃)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝐴𝐵/𝐴𝐶 = 7𝑥/(√113 𝑥) = 𝟕/(√𝟏𝟏𝟑 ) We have to find ((𝟏 + 𝐬𝐢𝐧⁡𝜽 ) (𝟏 −〖 𝐬𝐢𝐧〗⁡𝜽 ))/((𝟏 + 𝐜𝐨𝐬⁡𝜽 ) (𝟏 −〖 𝐜𝐨𝐬〗⁡𝜽 ) ) Using (a + b) (a – b) = a2 – b2 = ( (12 − 𝑠𝑖𝑛2 𝜃))/( (12 − 𝑐𝑜𝑠2𝜃)) = ( (1 − 𝑠𝑖𝑛2 𝜃))/( (1 − 𝑐𝑜𝑠2𝜃)) Putting sin 𝜽 = 𝟖/(√𝟏𝟏𝟑 ) & cos θ = 𝟕/(√𝟏𝟏𝟑 ) = ((1 − (8/(√113 ))^2 ))/((1 − (7/(√113 ))^2 ) ) = ((𝟏 − 𝟔𝟒/𝟏𝟏𝟑))/((𝟏 − 𝟒𝟗/𝟏𝟏𝟑) ) = (((113 − 64)/113))/(((113 − 49)/113) ) = (113 − 64)/(113 − 49 ) = 𝟒𝟗/(𝟔𝟒 ) Hence, ((𝟏 + 𝒔𝒊𝒏⁡𝜽)(𝟏 − 𝒔𝒊𝒏⁡𝜽))/((𝟏 + 𝒄𝒐𝒔⁡𝜽)(𝟏 − 𝒄𝒐𝒔⁡𝜽)) = 𝟒𝟗/(𝟔𝟒 ) Ex 8.1, 7 If cot θ = 7/8 , evaluate : (ii) cot2 θ Given cot θ = 7/8 So, cot2 θ = (7/8)^2 = 72/82 = 𝟒𝟗/𝟔𝟒