Question 5 - Area of quadrilateral - Chapter 7 Class 10 Coordinate Geometry

Transcript

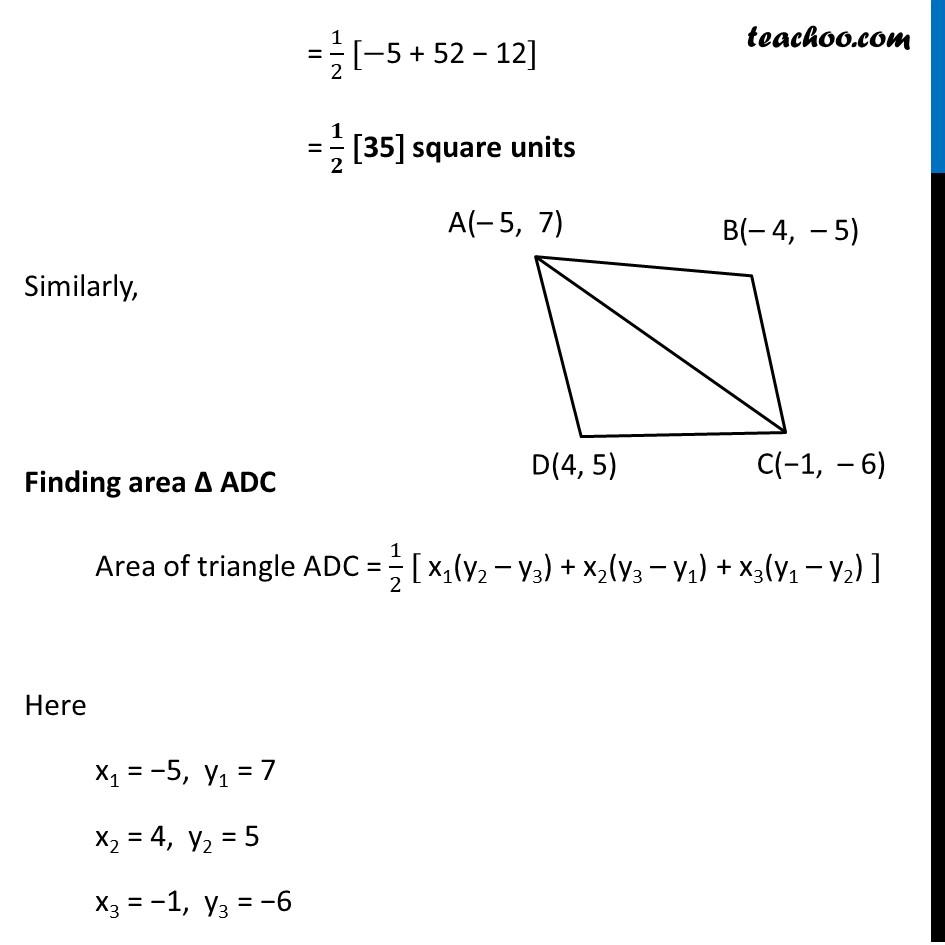
Question 5 If A(–5, 7), B(– 4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD. Let the vertices of quadrilateral be A(−5, 7) , B(−4, −5) C(−1, −6) , D(4, 5) Joining AC There are 2 triangles formed ABC & ACD Hence, Area of quadrilateral ABCD = Area of ∆ ABC + Area of ∆ ADC Finding area ∆ ABC Area of triangle ABC = 1/2 [ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) ] Here x1 = −5 , y1 = 7 x2 = −4 , y2 = −5 x3 = −1 , y3 = −6 Putting values Area of triangle ABC = 1/2 [ −5(−5 –(−6)) + (−4)(−6 – 7) + (−1)(7 – (−5)) ] = 1/2 [ −5(−5 + 6) – 4(−13) + (−1)(7 + 5)] = 1/2 [ −5(1) – 4(−13) + (−1)(12)] = 1/2 [−5 + 52 − 12] = 𝟏/𝟐 [35] square units Similarly, Finding area ∆ ADC Area of triangle ADC = 1/2 [ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) ] Here x1 = −5, y1 = 7 x2 = 4, y2 = 5 x3 = −1, y3 = −6 Area of triangle ADC = 1/2 [ −5(5 –(−6)) + 4(−6 – 7) + (−1)(7 – 5) ] = 1/2 [ −5(5 + 6) + 4(−13) + (−1)(2)] = 1/2 [ −5(11) + 4(−13) + (−1)(2)] = 1/2 [ −55 − 52 – 2] = 1/2 [ −109] But area cannot be negative, ∴ Area of triangle ADC = 𝟏/𝟐 [ 109] square units Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC = 1/2 [ 35 + 109] = 1/2 [ 144] = 72 square units