Solve all your doubts with Teachoo Black (new monthly pack available now!)
Example 10 - Chapter 7 Class 10 Coordinate Geometry (Term 1)
Last updated at Aug. 16, 2021 by Teachoo
Are you in school? Do you love Teachoo?
We would love to talk to you! Please fill this form so that we can contact you
Examples
Example 1
Example 2 Important
Example 3 Important
Example 4
Example 5 Important
Example 6
Example 7 Important
Example 8
Example 9 Important
Example 10 Important You are here
Example 11 Deleted for CBSE Board 2023 Exams
Example 12 Deleted for CBSE Board 2023 Exams
Example 13 Important Deleted for CBSE Board 2023 Exams
Example 14 Important Deleted for CBSE Board 2023 Exams
Example 15 Deleted for CBSE Board 2023 Exams
Chapter 7 Class 10 Coordinate Geometry
Serial order wise
Transcript
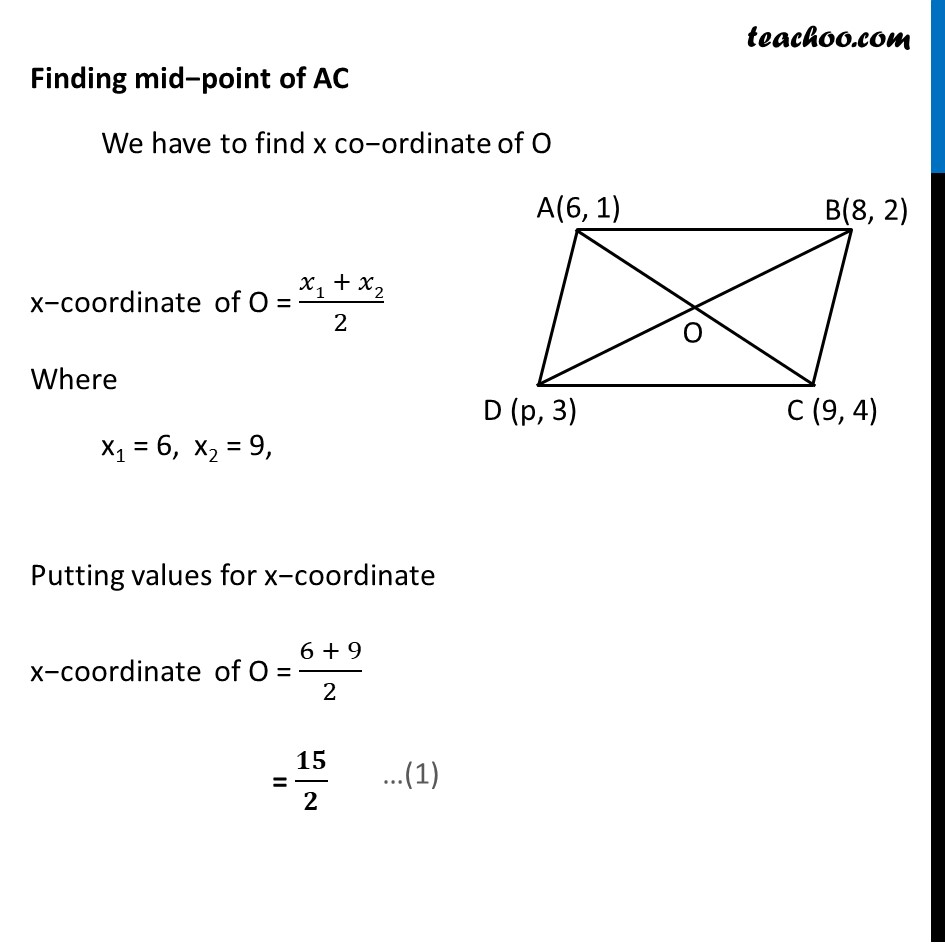
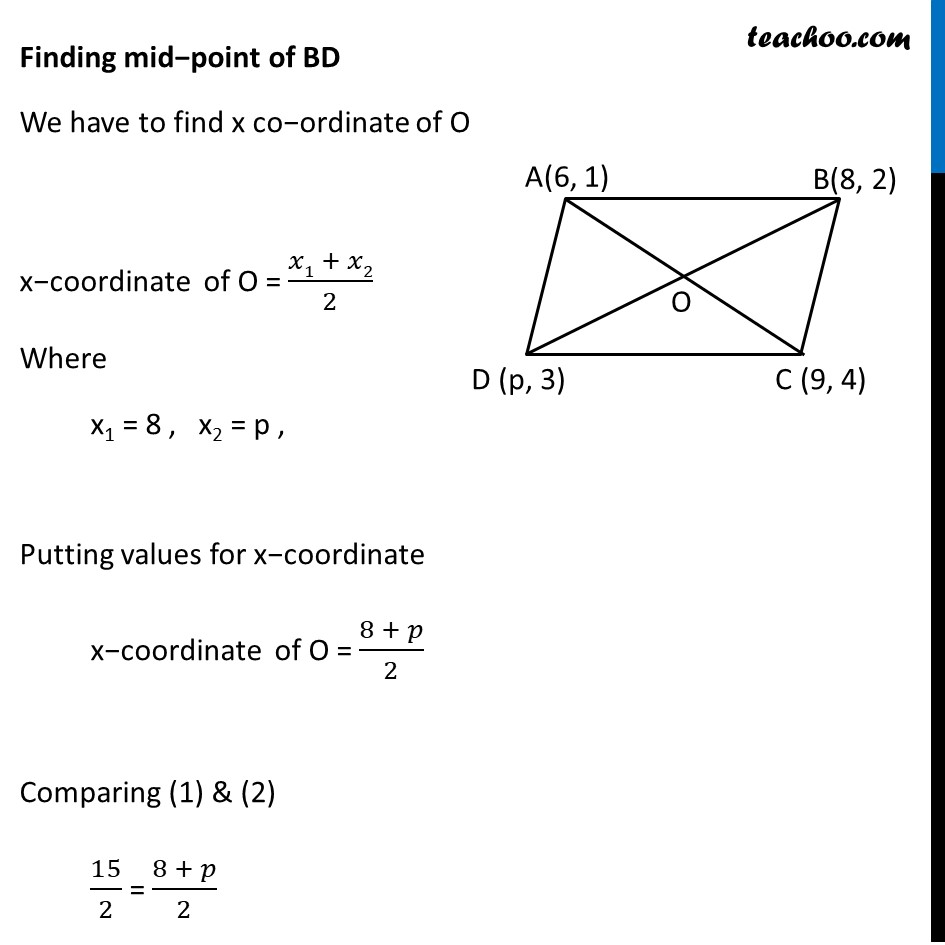
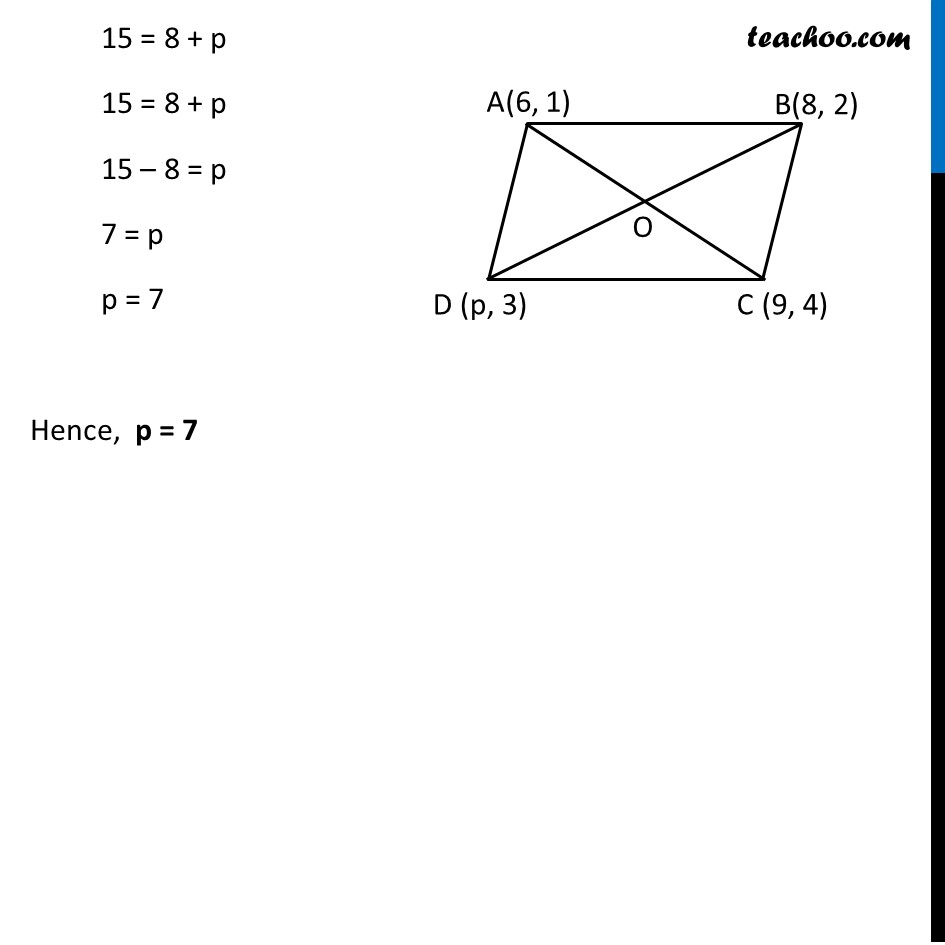
Example 10 If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p. Let the points be A(6, 1) , B(8, 2) C(9, 4) , D(p, 3) We know that diagonals of parallelogram bisect each other So, O is the mid−pint of AC & BD ∴ We find x co−ordinate of O from both AC & BD Finding mid−point of AC We have to find x co−ordinate of O x−coordinate of O = (𝑥1 + 𝑥2)/2 Where x1 = 6, x2 = 9, Putting values for x−coordinate x−coordinate of O = (6 + 9)/2 = 𝟏𝟓/𝟐 Finding mid−point of BD We have to find x co−ordinate of O x−coordinate of O = (𝑥1 + 𝑥2)/2 Where x1 = 8 , x2 = p , Putting values for x−coordinate x−coordinate of O = (8 + 𝑝)/2 Comparing (1) & (2) 15/2 = (8 + 𝑝)/2 15 = 8 + p 15 = 8 + p 15 – 8 = p 7 = p p = 7 Hence, p = 7
