
Section Formula- Finding coordinates of a point in a quadrilateral
Section Formula- Finding coordinates of a point in a quadrilateral
Last updated at Dec. 13, 2024 by Teachoo




Transcript
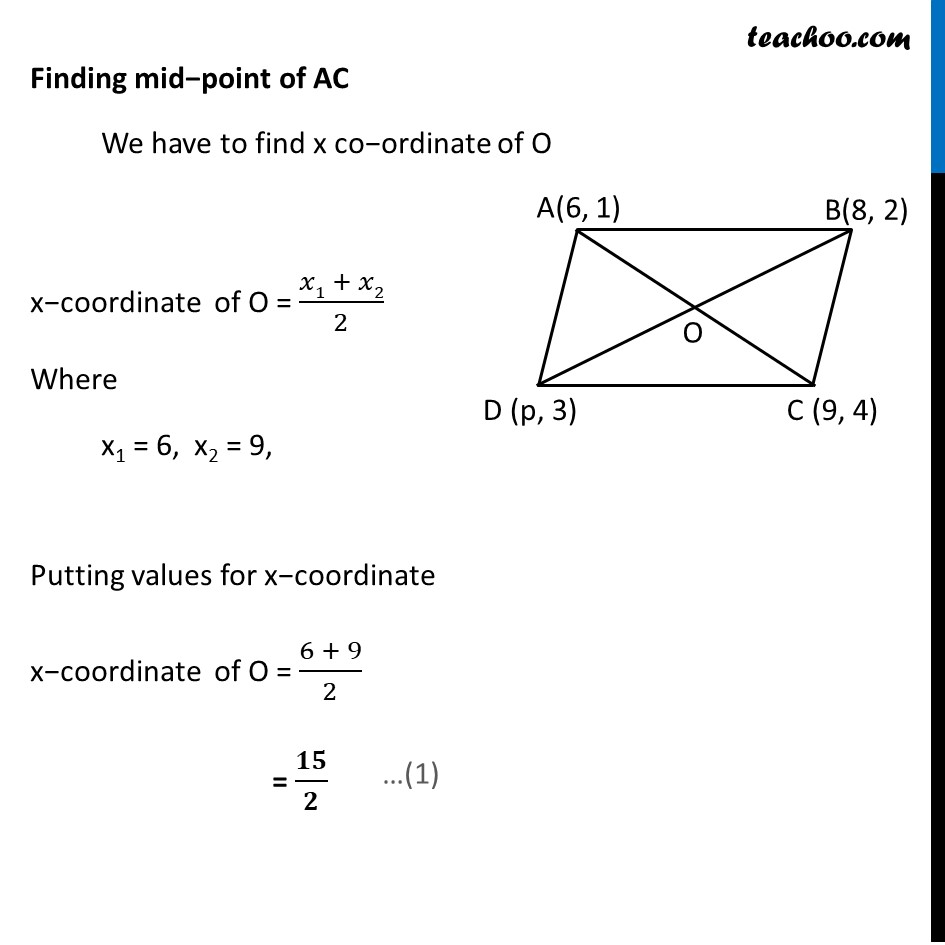
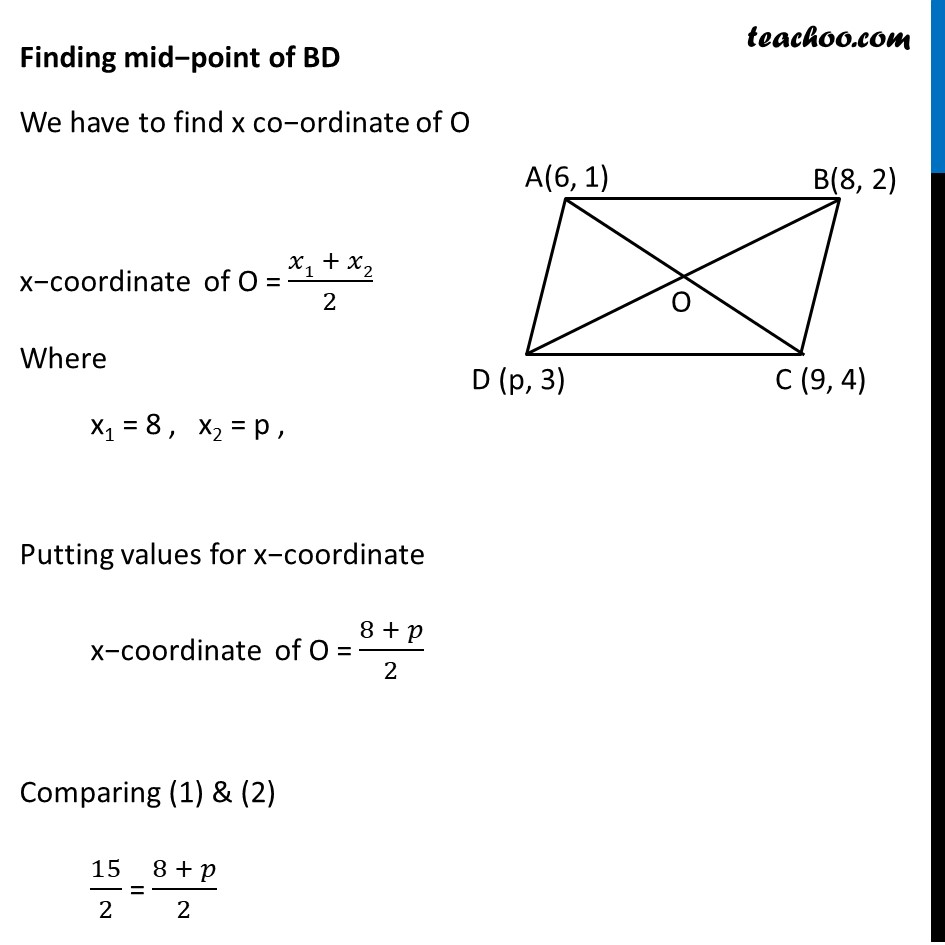
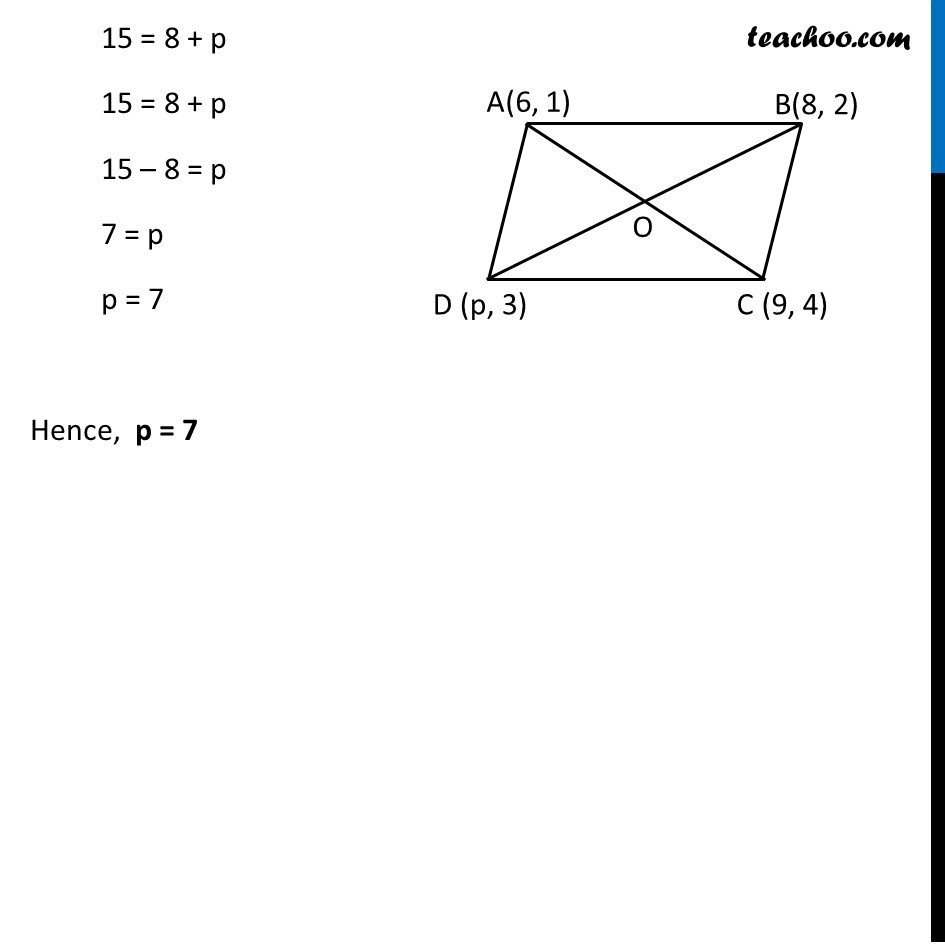
Example 10 If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p. Let the points be A(6, 1) , B(8, 2) C(9, 4) , D(p, 3) We know that diagonals of parallelogram bisect each other So, O is the mid−pint of AC & BD ∴ We find x co−ordinate of O from both AC & BD Finding mid−point of AC We have to find x co−ordinate of O x−coordinate of O = (𝑥1 + 𝑥2)/2 Where x1 = 6, x2 = 9, Putting values for x−coordinate x−coordinate of O = (6 + 9)/2 = 𝟏𝟓/𝟐 Finding mid−point of BD We have to find x co−ordinate of O x−coordinate of O = (𝑥1 + 𝑥2)/2 Where x1 = 8 , x2 = p , Putting values for x−coordinate x−coordinate of O = (8 + 𝑝)/2 Comparing (1) & (2) 15/2 = (8 + 𝑝)/2 15 = 8 + p 15 = 8 + p 15 – 8 = p 7 = p p = 7 Hence, p = 7