You are here
Ex 7.2, 10 - Chapter 7 Class 10 Coordinate Geometry
Last updated at Dec. 13, 2024 by Teachoo
Distance Formula
Chapter 7 Class 10 Coordinate Geometry
Concept wise
-
Distance Formula
- Equidistant points
- Checking points collinear or not
- Type of triangle formed
- Type of quadrilateral formed
- Section Formula- Finding coordinates
- Section Formula- Finding coordinates of a point in a quadrilateral
- Finding ratio
- Area of triangle
- Given area, finding k
- Area of quadrilateral
Transcript
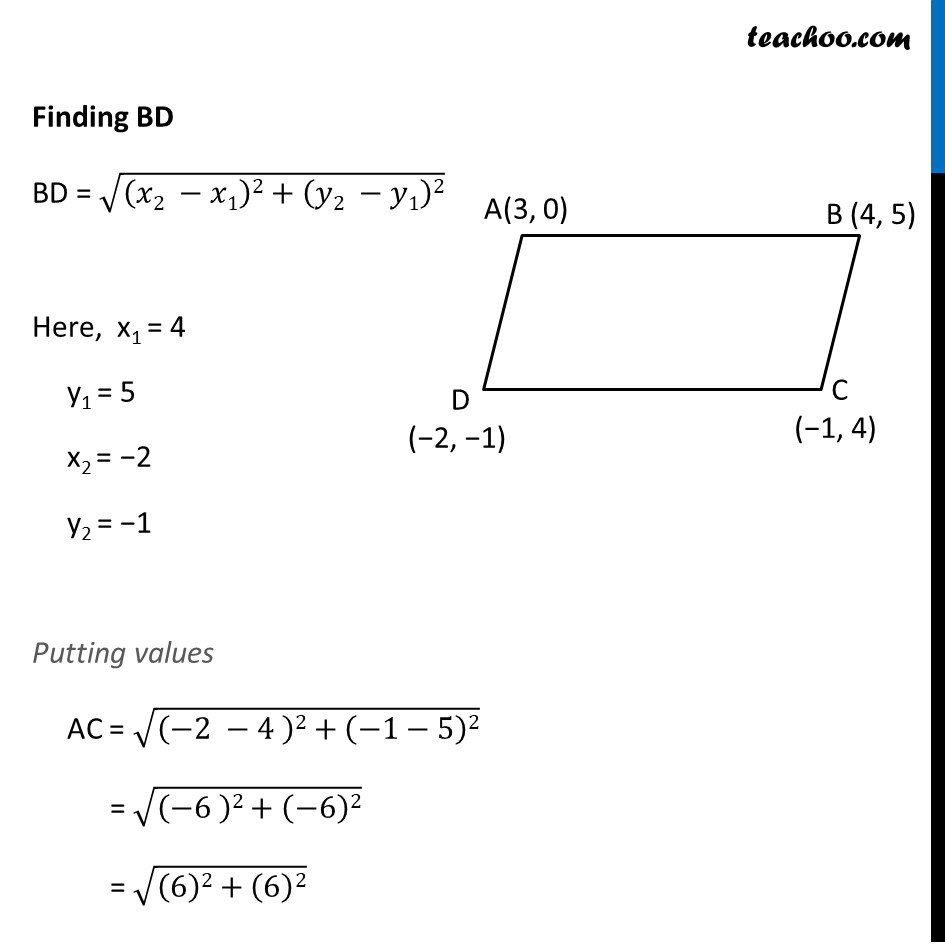
Ex 7.2, 10 Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order. [Hint : Area of a rhombus = 1/2 (product of its diagonals)] Let the vertices be A (3, 0) , B (4, 5) C (−1, 4) , D (−2, −1) We know that Area of Rhombus = 1/2 (Product of diagonals) = 1/2 × AC × BD We need to find AC & BD using distance formula Finding AC AC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) Here, x1 = 3 , y1 = 0 x2 = −1, y2 = 4 Putting values AC = √((−1−3 )2+(4 −0)2) = √((−4 )2+(4)2) = √((4 )2+(4)2) = √(2(4)2) = √2 × 4 = 4√2 Finding BD BD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) Here, x1 = 4 y1 = 5 x2 = −2 y2 = −1 Putting values AC = √((−2 −4 )2+(−1−5)2) = √((−6 )2+(−6)2) = √((6)2+(6)2) = √(2(6)2) = √2 × 6 = 6√2 Now, Area of Rhombus = 1/2 × AC × BD = 1/2 × 4√2 × 6√2 = 2√2 × 6√2 = (2 × 6) × (√2 × √2) = (12) × (2) = 24 square units Hence, Area of rhombus = 24 square units
