Question 2 - Area of similar triangles - Chapter 6 Class 10 Triangles

Transcript

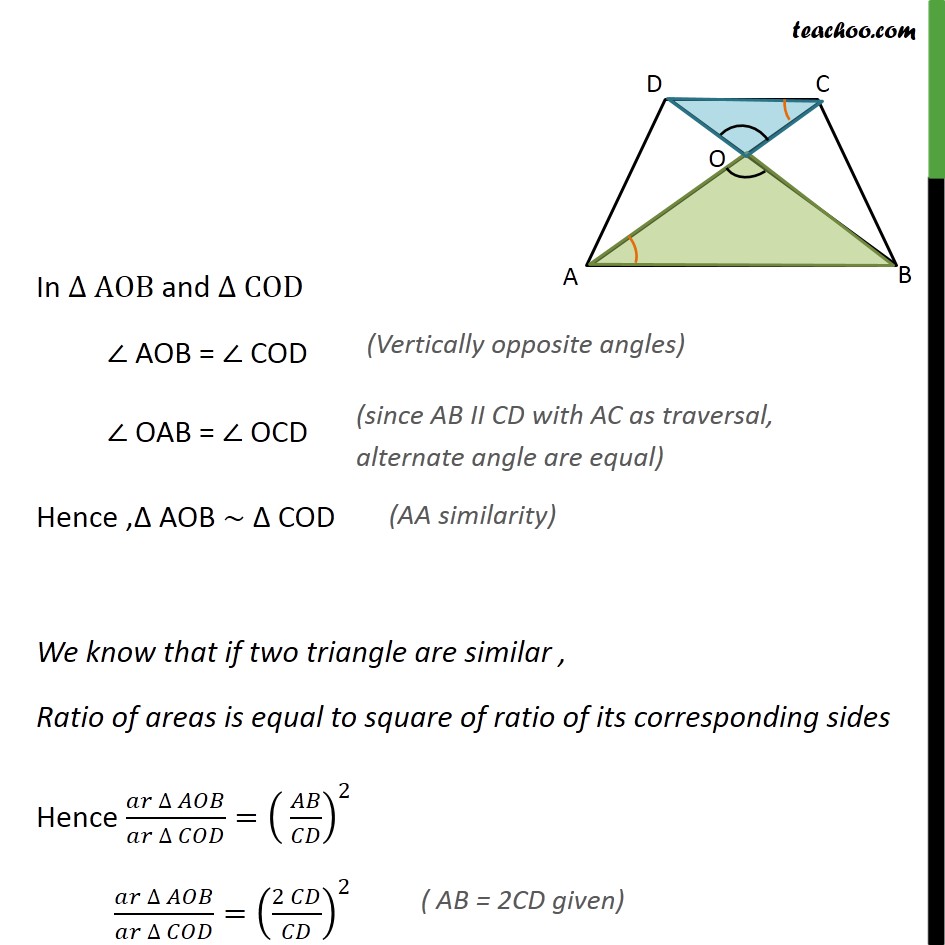
Question 2 Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD. Given: ABCD is trapezium where AB II DC and diagonals intersect at O & AB = 2 CD To find: (ar ∆ AOB)/(ar ∆ COD) Solution: Since we need to find ratio of area of ∆ 𝐴𝑂𝐵 and ∆ 𝐶𝑂𝐷. Lets first prove ∆ 𝐴𝑂𝐵 and ∆ 𝐶𝑂𝐷 are similar In ∆ AOB and ∆ COD ∠ AOB = ∠ COD ∠ OAB = ∠ OCD Hence ,Δ AOB ~ Δ COD We know that if two triangle are similar , Ratio of areas is equal to square of ratio of its corresponding sides Hence (𝑎𝑟 ∆ 𝐴𝑂𝐵)/(𝑎𝑟 ∆ 𝐶𝑂𝐷)=( 𝐴𝐵/𝐶𝐷)^2 (𝑎𝑟 ∆ 𝐴𝑂𝐵)/(𝑎𝑟 ∆ 𝐶𝑂𝐷)=((2 𝐶𝐷)/𝐶𝐷)^2 (𝑎𝑟 ∆ 𝐴𝑂𝐵)/(𝑎𝑟 ∆ 𝐶𝑂𝐷)=((2 )/1)^2 (𝑎𝑟 ∆ 𝐴𝑂𝐵)/(𝑎𝑟 ∆ 𝐶𝑂𝐷)=4/1 ∴ ar Δ AOB : ar Δ COD =4:1 Hence ratio of areas is 4 :1