Ex 6.3, 14 - Chapter 6 Class 10 Triangles (Important Question)

Transcript

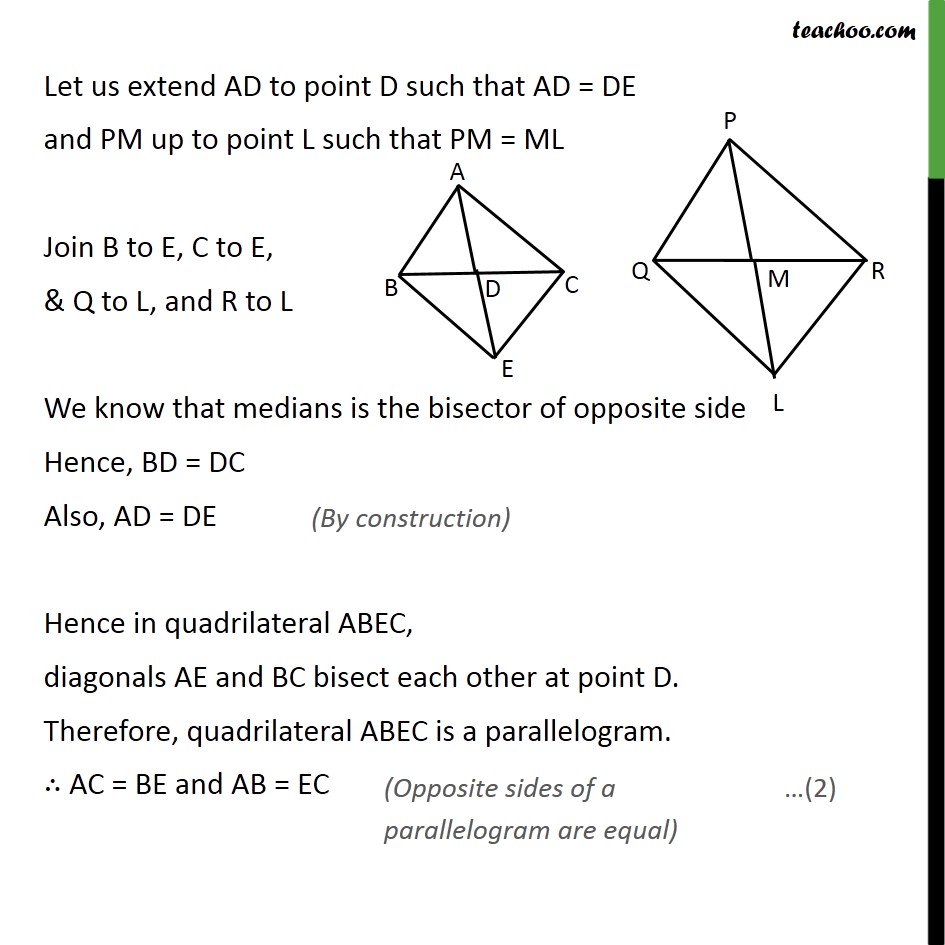
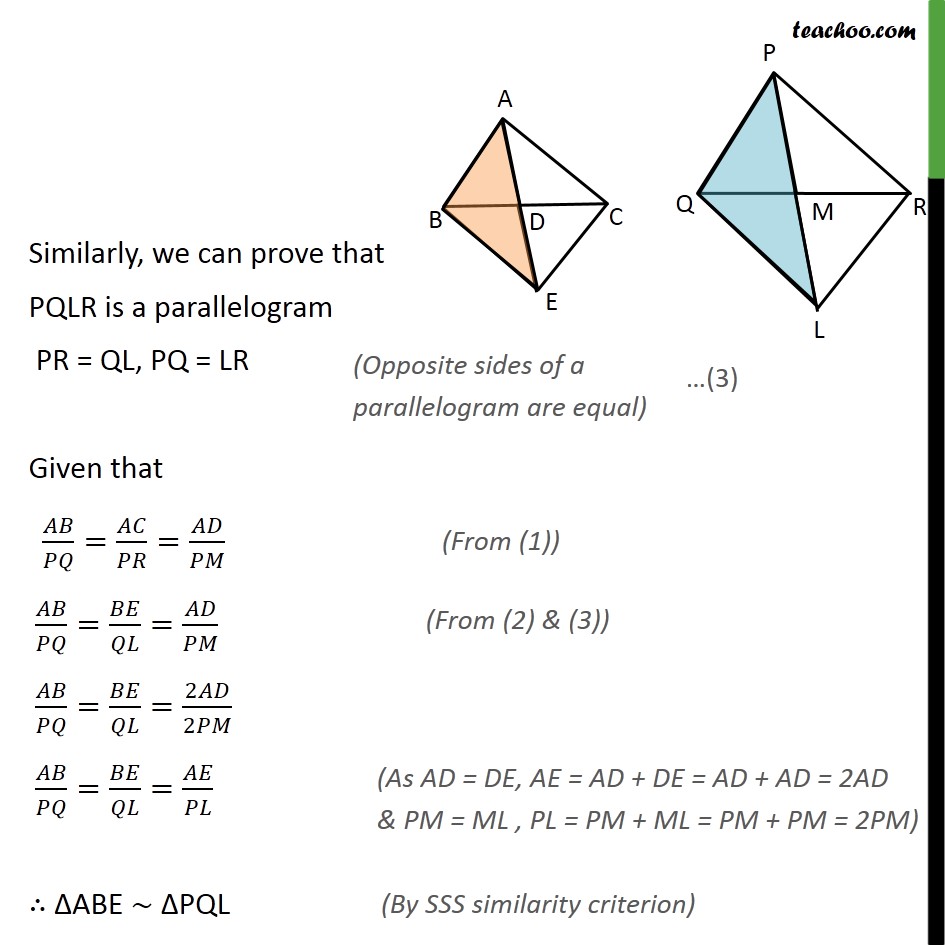
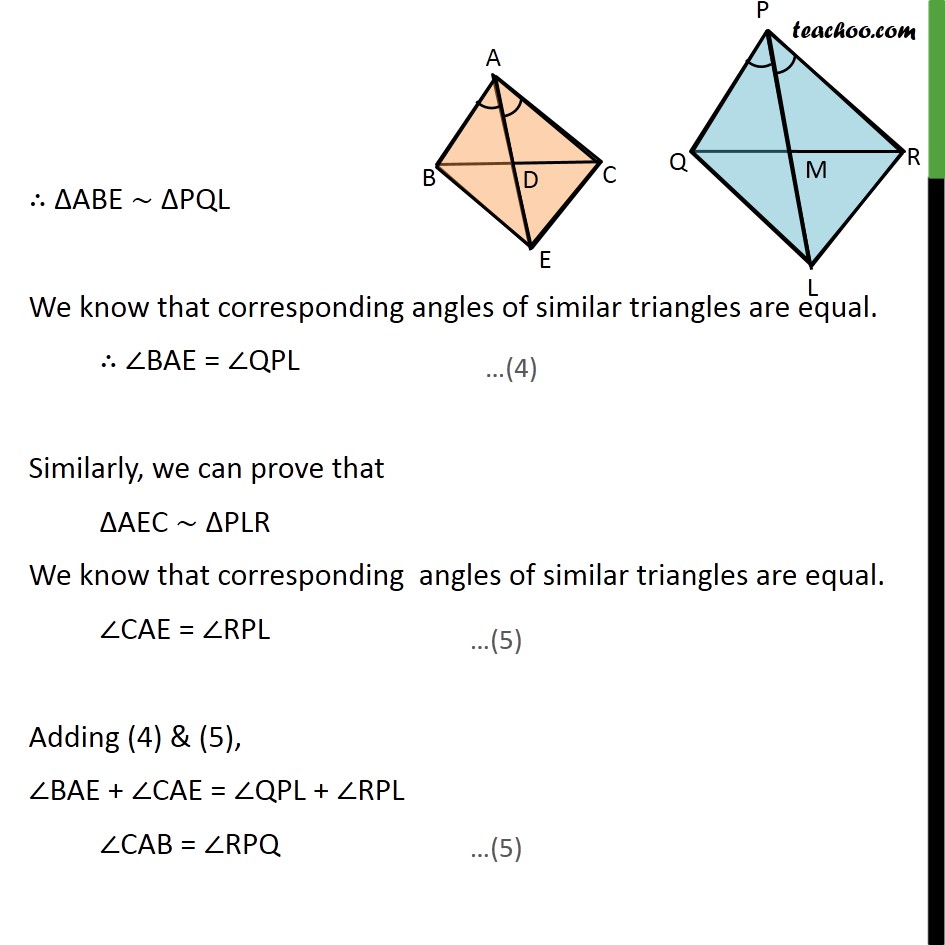
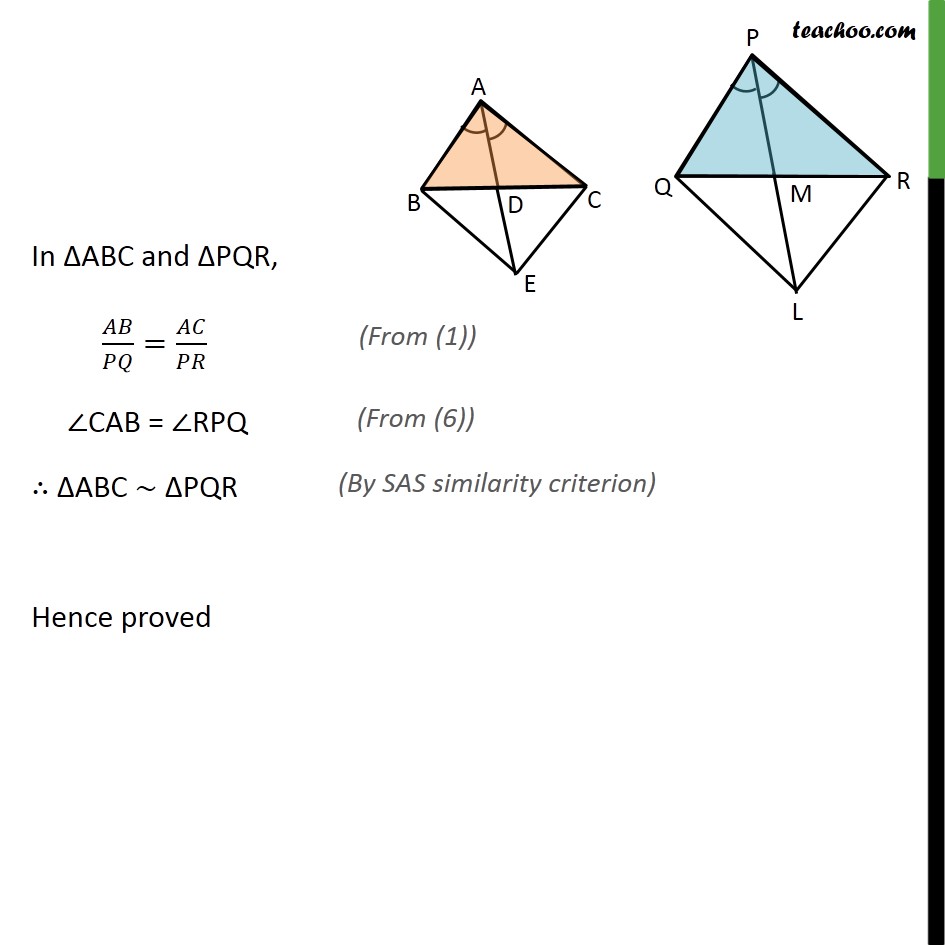
Ex 6.3, 14 Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ABC PQR. Given: ABC and PQR AD is the median of ABC ,PM is the median of PQR / = / = / To Prove:- ABC PQR. Proof: Let us extend AD to point D such that AD = DE and PM up to point L such that PM = ML Join B to E, C to E, & Q to L, and R to L We know that medians is the bisector of opposite side Hence, BD = DC Also, AD = DE Hence in quadrilateral ABEC, diagonals AE and BC bisect each other at point D. Therefore, quadrilateral ABEC is a parallelogram. AC = BE and AB = EC Similarly, we can prove that PQLR is a parallelogram PR = QL, PQ = LR Given that / = / = / / = / = / / = / =2 /2 / = / = / ABE PQL ABE PQL We know that corresponding angles of similar triangles are equal. BAE = QPL Similarly, we can prove that AEC PLR We know that corresponding angles of similar triangles are equal. CAE = RPL Adding (4) & (5), BAE + CAE = QPL + RPL CAB = RPQ In ABC and PQR, / = / CAB = RPQ ABC PQR Hence proved