Ex 6.3, 13 - Chapter 6 Class 10 Triangles (Important Question)

Last updated at Dec. 13, 2024 by

Ex 6.3, 13 - D is a point on side BC of a triangle ABC - AA Similarity

Ex 6.3, 13 - Chapter 6 Class 10 Triangles - Part 2

Go Ad-free

Transcript

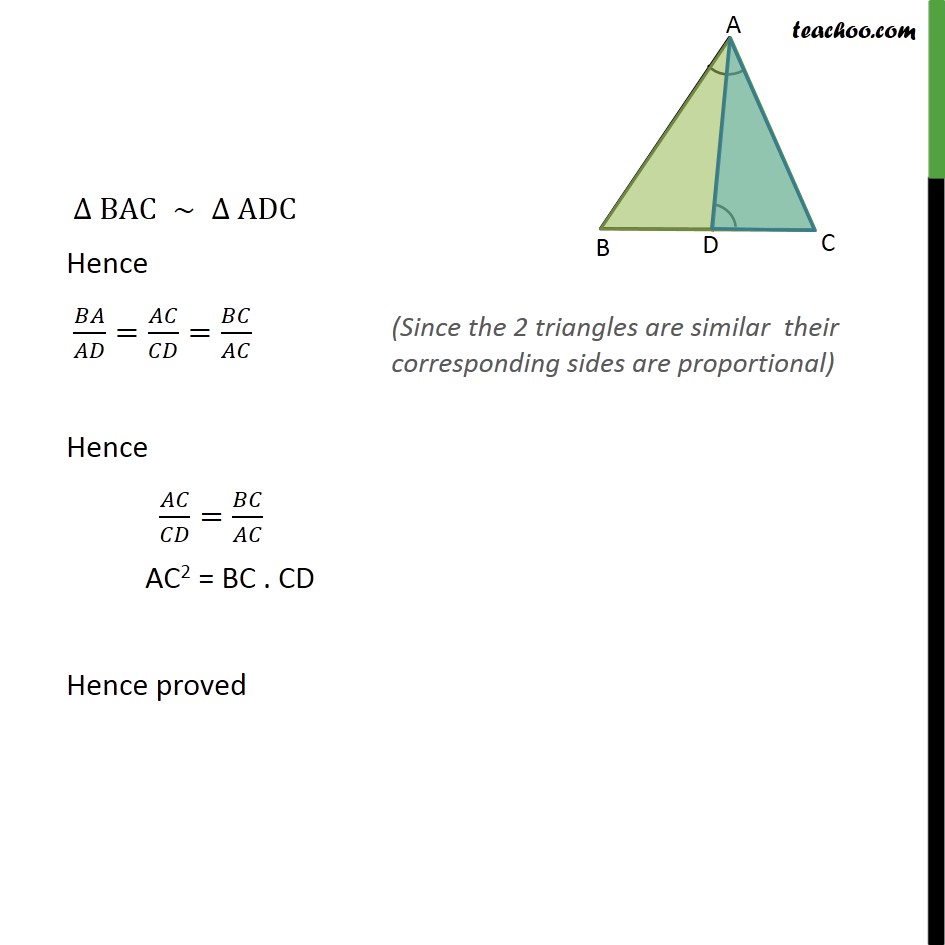
Ex 6.3, 13 D is a point on the side BC of a triangle ABC such that ADC = BAC. Show that CA2 = CB.CD Given: ABC where ADC = BAC To Prove: CA2 = CB.CD i.e. / = / Proof:- In BAC and ADC ACB = ACD BAC = ADC Hence by AA similarity criterion BAC ADC BAC ADC Hence / = / = / Hence / = / AC2 = BC . CD Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo